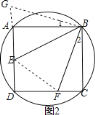
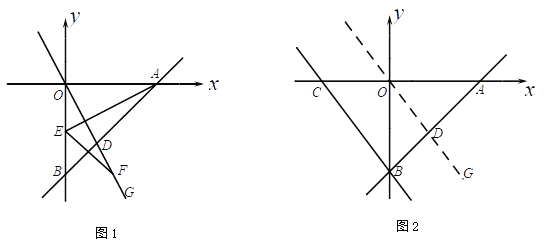题目内容
【题目】如图,四边形![]() 是
是![]() 的内接四边形,
的内接四边形,![]() ,点
,点![]() 、
、![]() 分别是弦
分别是弦![]() 、
、![]() 上的点.
上的点.

![]() 若
若![]() ,
,![]() .求证:
.求证:![]() 是
是![]() 的直径.
的直径.
![]() 若
若![]() ,
,![]() ,
,![]() .求
.求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)首先证明△ABE≌△BCF, 得到∠A=∠C,再根据圆内接四边形的性质,得到∠A+∠C=180°, 由圆周角定理即可得到结论;
(2)首先证出四边形ABCD是正方形,接下来延长DA到G,使AG=CF,如图,推出△ABG≌△CBF,△GBE≌△FBE,然后根据勾股定理列方程即可得到结论.
![]() 证明:∵
证明:∵![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
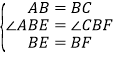 ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是
是![]() 的内接四边形,
的内接四边形,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的直径;
的直径;![]() 解:∵
解:∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
如图![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,
,
在![]() 与
与![]() 中,
中,
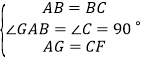 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]()
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目