题目内容
 如图,已知点A1,A2,…,A2015在函数y=x2位于第二象限的图象上,点B1,B2,…,B2015在函数y=x2位于第一象限的图象上,点C1,C2,…,C2015在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2014A2015C2015B2015都是正方形,则正方形C2014A2015C2015B2015的边长为( )
如图,已知点A1,A2,…,A2015在函数y=x2位于第二象限的图象上,点B1,B2,…,B2015在函数y=x2位于第一象限的图象上,点C1,C2,…,C2015在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2014A2015C2015B2015都是正方形,则正方形C2014A2015C2015B2015的边长为( )| A、2014 | ||
| B、2015 | ||
C、2014
| ||
D、2015
|
考点:二次函数图象上点的坐标特征,正方形的性质
专题:规律型
分析:作B1D⊥y轴与D,B2E⊥y轴于E,如图,根据正方形的性质得到△ODB1为等腰直角三角形,则可设B1(t,t),把B1(t,t)代入y=x2解得t1=0,t2=1,得到B1(1,1),根据正方形的性质得C1(0,2),再设B2(m,m+2),把B2(m,m+2)代入y=x2解得m1=2,m2=-1,得到B2(2,4),由此规律得到B2015(2015,20152),然后根据正方形的计算边长.
解答:解: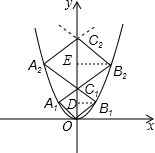 作B1D⊥y轴与D,B2E⊥y轴于E,如图,
作B1D⊥y轴与D,B2E⊥y轴于E,如图,
∵四边形OA1C1B1是正方形,
∴△ODB1为等腰直角三角形,
设B1(t,t),
把B1(t,t)代入y=x2得t2=t,解得t1=0,t2=1,
∴B1(1,1),
∴C1(0,2),
设B2(m,m+2),
把B2(m,m+2)代入y=x2得m2=m+2,解得m1=2,m2=-1,
∴B2(2,4),
∴B2015(2015,20152),
∴正方形C2014A2015C2015B2015的边长=2015
.
故选D.
 作B1D⊥y轴与D,B2E⊥y轴于E,如图,
作B1D⊥y轴与D,B2E⊥y轴于E,如图,∵四边形OA1C1B1是正方形,
∴△ODB1为等腰直角三角形,
设B1(t,t),
把B1(t,t)代入y=x2得t2=t,解得t1=0,t2=1,
∴B1(1,1),
∴C1(0,2),
设B2(m,m+2),
把B2(m,m+2)代入y=x2得m2=m+2,解得m1=2,m2=-1,
∴B2(2,4),
∴B2015(2015,20152),
∴正方形C2014A2015C2015B2015的边长=2015
| 2 |
故选D.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了正方形的性质.

练习册系列答案
相关题目
如果x:(x+y)=3:5,那么x:y=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 点A,B在数轴上分别表示有理数a,b,A,B两点之间的距离表示为AB,回答下列问题:
点A,B在数轴上分别表示有理数a,b,A,B两点之间的距离表示为AB,回答下列问题:
 实数a,b在数轴上表示如下图:则下列结论正确的有
实数a,b在数轴上表示如下图:则下列结论正确的有