题目内容
如图所示，⊙O的直径AB=16cm，P是OB的中点，∠APC=30°，求CD的长．
【答案】分析：连接半径作弦心距，构造出直角三角形利用勾股定理就可以求出一直角边（即弦CD的一半）．
解答：
解：过O作OE⊥CD，垂足为E，连接OC，
∵AB=16cm，
∴OC=OB=8cm，
∵P是OB的中点，
∴OP=
OB=4cm，
∵∠APC=30°，OE⊥CD，
∴OE=
OP=2cm，
在Rt△COE中CE=
=
=2
cm，
∴CD=2CE=4
cm．
点评：作辅助线构造直角三角形是解决本题的突破点．
解答：
解：过O作OE⊥CD，垂足为E，连接OC，∵AB=16cm，
∴OC=OB=8cm，
∵P是OB的中点，
∴OP=
OB=4cm，∵∠APC=30°，OE⊥CD，
∴OE=
OP=2cm，在Rt△COE中CE=
==2cm，∴CD=2CE=4
cm．点评：作辅助线构造直角三角形是解决本题的突破点．
练习册系列答案
阅读快车系列答案
相关题目
为C，连接AC．
点D，C，设AD=x，BC=y．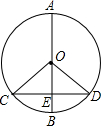
如图所示，⊙O的直径AB垂直于弦CD，AB、CD相交于点E，∠COD=100°，求∠COE，∠D的度数．
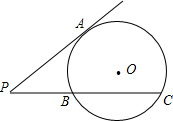如图所示，⊙O的直径的长是关于x的二次方程x2+2（k-2）x+k=0（k是整数）的最大整数根． P是⊙O外一点，过点P作⊙O的切线PA和割线PBC，其中A为切点，点B，C是直线PBC与⊙O的交点．若PA，PB，PC的长都是正整数，且PB的长不是合数，求PA2+PB2+PC2的值．
如图所示，⊙O的直径AB和弦CD交于E，已知AE=6cm，EB=2cm，∠CEA=30°，求圆心O到CD的距离．