题目内容
如图，直线y=-2x+10与x轴、y轴分别交于A、B两点，把△ABC沿AB翻折，点O落在C处，则点C的坐标是
- A.（9，3）
- B.（8，4）
- C.（10，5）
- D.（5+
，2）
B
分析：由直线解析式求得A、B两点的坐标，然后求得线段AB的长，利用翻折对称不变性，求得C点的坐标．
解答：令y=-2x+10=0，
解得：x=5，
∴A点的坐标为：（5，0），
令x=0，得y=10，
∴B点的坐标为：（0，10）
∴OA=5，OB=10，
∴AB=5，
连接OC交AB于D点，作DE⊥x轴于E，作DF⊥y轴于F．
∴OD=
×5×10÷（×5）=2，
∵OA2=AD•AB
∴AD=
=
=．
∵△ADE∽△ABO
∴
=
∴DE=OB=×10=2，
AE=OA=×5=1
则OE=4
∴点D的坐标是（4，2）．
∵D是OC的中点．
∴点C的坐标是（8，4）．
故选B．
点评：本题考查了勾股定理、一次函数性质及相似三角形的知识，看似简单的一道小题，实际上是一道不错的综合题．
分析：由直线解析式求得A、B两点的坐标，然后求得线段AB的长，利用翻折对称不变性，求得C点的坐标．
解答：令y=-2x+10=0，
解得：x=5，
∴A点的坐标为：（5，0），
令x=0，得y=10，
∴B点的坐标为：（0，10）
∴OA=5，OB=10，
∴AB=5
，连接OC交AB于D点，作DE⊥x轴于E，作DF⊥y轴于F．
∴OD=
×5×10÷（×5）=2，∵OA2=AD•AB
∴AD=
==．∵△ADE∽△ABO
∴
=∴DE=
OB=×10=2，AE=
OA=×5=1则OE=4
∴点D的坐标是（4，2）．
∵D是OC的中点．
∴点C的坐标是（8，4）．
故选B．
点评：本题考查了勾股定理、一次函数性质及相似三角形的知识，看似简单的一道小题，实际上是一道不错的综合题．
练习册系列答案
教材全解字词句篇系列答案
相关题目
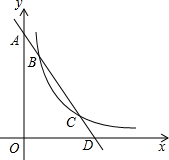如图，直线y=-2x+b与y轴交于点A，与x轴交于点D，与双曲线
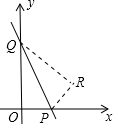如图，直线y=-2x+6与x轴、y轴分别交于P、Q两点，把△POQ沿PQ翻折，点O落在R处，则点R的坐标是
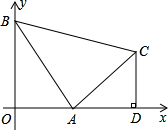腰直角△ABC，∠BAC=90°，过C作CD⊥x轴，垂足为D．
轴分别交于点C、D．直线EB交x轴于点F．
如图，直线y=-2x+8与两坐标轴分别交于P，Q两点，在线段PQ上有一点A，过点A分别作两坐标轴的垂线，垂足分别为B、C．