题目内容
如图,一直线AC与已知直线AB: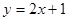 关于y轴对称。
关于y轴对称。
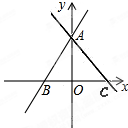
(1)求直线AC的解析式;
(2)说明两直线与x轴围成的三角形是等腰三角形。
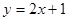 关于y轴对称。
关于y轴对称。
(1)求直线AC的解析式;
(2)说明两直线与x轴围成的三角形是等腰三角形。
(1) ;(2)由BO=CO,∠AOB=∠AOC=90°,再结合公共边AO即可证得△AOB≌△AOC,即可证得结论.
;(2)由BO=CO,∠AOB=∠AOC=90°,再结合公共边AO即可证得△AOB≌△AOC,即可证得结论.
 ;(2)由BO=CO,∠AOB=∠AOC=90°,再结合公共边AO即可证得△AOB≌△AOC,即可证得结论.
;(2)由BO=CO,∠AOB=∠AOC=90°,再结合公共边AO即可证得△AOB≌△AOC,即可证得结论.试题分析:(1)先求出直线AB:
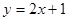 与坐标轴的交点A、B,再根据轴对称的性质即可求得点C的坐标,设直线AC的解析式为
与坐标轴的交点A、B,再根据轴对称的性质即可求得点C的坐标,设直线AC的解析式为 ,根据待定系数法即可求得结果;
,根据待定系数法即可求得结果;(2)由BO=CO,∠AOB=∠AOC=90°,再结合公共边AO即可证得△AOB≌△AOC,即可证得结论.
(1)在直线AB:
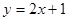 中,当
中,当 时,
时, ,当
,当 时,
时,
则A点坐标为(0,1),B点坐标为(
 ,0)
,0)根据轴对称的性质可得C点坐标为(
 ,0)
,0)设直线AC的解析式为

∵图象过点A(0,1),C(
 ,0)
,0)∴
 ,解得
,解得
∴直线AC的解析式为
 ;
;(2)∵BO=CO,∠AOB=∠AOC=90°,AO=AO
∴△AOB≌△AOC
∴AB=AC
∴两直线与x轴围成的三角形是等腰三角形.
点评:解题的关键是熟练掌握函数图象上的适合函数关系式,即代入关系式后能使左右两边相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 是一次函数
是一次函数 的图象,直线
的图象,直线 是一次函数
是一次函数

 、
、 、
、 三点坐标。(2)求
三点坐标。(2)求 的面积。
的面积。
 ,点E在坐标轴上,请画出符合题意的图形;(注意两解哦!)
,点E在坐标轴上,请画出符合题意的图形;(注意两解哦!)
 上,△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,求A2013 的横坐标 .
上,△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,求A2013 的横坐标 . 