题目内容
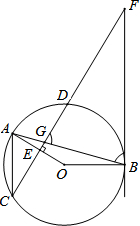 如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.
如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.
(1)若∠FGB=∠FBG,求证:BF是⊙O的切线;
(2)若tan∠F= ,CD=a,请用a表示⊙O的半径;
,CD=a,请用a表示⊙O的半径;
(3)求证:GF2-GB2=DF•GF.
(1)证明:∵OA=OB,
∴∠OAB=∠OBA,
∵OA⊥CD,
∴∠OAB+∠AGC=90°,
又∵∠FGB=∠FBG,∠FGB=∠AGC,
∴∠FBG+∠OBA=90°,
即∠OBF=90°,
∴OB⊥FB,
∵AB是⊙O的弦,
∴点B在⊙O上,
∴BF是⊙O的切线;
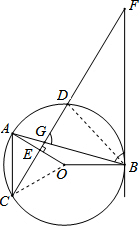
(2)解:∵AC∥BF,
∴∠ACF=∠F,
∵CD=a,OA⊥CD,
∴CE= CD=
CD= a,
a,
∵tan∠F= ,
,
∴tan∠ACF= =
= ,
,
即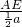 =
= ,
,
解得AE= a,
a,
连接OC,设圆的半径为r,则OE=r- a,
a,
在Rt△OCE中,CE2+OE2=OC2,
即( a)2+(r-
a)2+(r- a)2=r2,
a)2=r2,
解得r=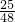 a;
a;
(3)证明:连接BD,
∵∠DBG=∠ACF,∠ACF=∠F(已证),
∴∠DBG=∠F,
又∵∠FGB=∠BGF,
∴△BDG∽△FBG,
∴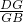 =
=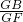 ,
,
即GB2=DG•GF,
∴GF2-GB2=GF2-DG•GF=GF(GF-DG)=GF•DF,
即GF2-GB2=DF•GF.
分析:(1)根据等边对等角可得∠OAB=∠OBA,然后根据OA⊥CD得到∠OAB+∠AGC=90°推出∠FBG+∠OBA=90°,从而得到OB⊥FB,再根据切线的定义证明即可;
(2)根据两直线平行,内错角相等可得∠ACF=∠F,根据垂径定理可得CE= CD=
CD= a,连接OC,设圆的半径为r,表示出OE,然后利用勾股定理列式计算即可求出r;
a,连接OC,设圆的半径为r,表示出OE,然后利用勾股定理列式计算即可求出r;
(3)连接BD,根据在同圆或等圆中,同弧所对的圆周角相等可得∠DBG=∠ACF,然后求出∠DBG=∠F,从而求出△BDG和△FBG相似,根据相似三角形对应边成比例列式表示出BG2,然后代入等式左边整理即可得证.
点评:本题是圆的综合题型,主要考查了切线的证明,解直角三角形,勾股定理的应用,相似三角形的判定与性质,作辅助线构造出直角三角形与相似三角形是解题的关键,(3)的证明比较灵活,想到计算整理后得证是解题的关键.
∴∠OAB=∠OBA,
∵OA⊥CD,
∴∠OAB+∠AGC=90°,
又∵∠FGB=∠FBG,∠FGB=∠AGC,
∴∠FBG+∠OBA=90°,
即∠OBF=90°,
∴OB⊥FB,
∵AB是⊙O的弦,
∴点B在⊙O上,
∴BF是⊙O的切线;

(2)解:∵AC∥BF,
∴∠ACF=∠F,
∵CD=a,OA⊥CD,
∴CE=
 CD=
CD= a,
a,∵tan∠F=
 ,
,∴tan∠ACF=
 =
= ,
,即
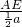 =
= ,
,解得AE=
 a,
a,连接OC,设圆的半径为r,则OE=r-
 a,
a,在Rt△OCE中,CE2+OE2=OC2,
即(
 a)2+(r-
a)2+(r- a)2=r2,
a)2=r2,解得r=
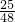 a;
a;(3)证明:连接BD,
∵∠DBG=∠ACF,∠ACF=∠F(已证),
∴∠DBG=∠F,
又∵∠FGB=∠BGF,
∴△BDG∽△FBG,
∴
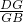 =
=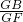 ,
,即GB2=DG•GF,
∴GF2-GB2=GF2-DG•GF=GF(GF-DG)=GF•DF,
即GF2-GB2=DF•GF.
分析:(1)根据等边对等角可得∠OAB=∠OBA,然后根据OA⊥CD得到∠OAB+∠AGC=90°推出∠FBG+∠OBA=90°,从而得到OB⊥FB,再根据切线的定义证明即可;
(2)根据两直线平行,内错角相等可得∠ACF=∠F,根据垂径定理可得CE=
 CD=
CD= a,连接OC,设圆的半径为r,表示出OE,然后利用勾股定理列式计算即可求出r;
a,连接OC,设圆的半径为r,表示出OE,然后利用勾股定理列式计算即可求出r;(3)连接BD,根据在同圆或等圆中,同弧所对的圆周角相等可得∠DBG=∠ACF,然后求出∠DBG=∠F,从而求出△BDG和△FBG相似,根据相似三角形对应边成比例列式表示出BG2,然后代入等式左边整理即可得证.
点评:本题是圆的综合题型,主要考查了切线的证明,解直角三角形,勾股定理的应用,相似三角形的判定与性质,作辅助线构造出直角三角形与相似三角形是解题的关键,(3)的证明比较灵活,想到计算整理后得证是解题的关键.

练习册系列答案
相关题目
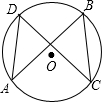 已知:如图,在⊙O中,弦AD=BC.求证:AB=CD.
已知:如图,在⊙O中,弦AD=BC.求证:AB=CD. 4、如图,在⊙O中,弦BC∥半径OA,AC与OB相交于M,∠C=20°,则∠AMB的度数为( )
4、如图,在⊙O中,弦BC∥半径OA,AC与OB相交于M,∠C=20°,则∠AMB的度数为( ) 标系.
标系. 如图,在⊙O中,弦AB=BC=CD,且∠ABC=140°,则∠AED=( )
如图,在⊙O中,弦AB=BC=CD,且∠ABC=140°,则∠AED=( ) 如图,在⊙O中,弦AB与CD相交于点P,连接AC、DB.
如图,在⊙O中,弦AB与CD相交于点P,连接AC、DB.