Question

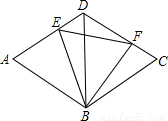
已知菱形ABCD的对角线AC和BD相交于点O，AC=2a，BD=2b，AB=c
（1）菱形的对角线AC和BD具有怎样的位置关系？
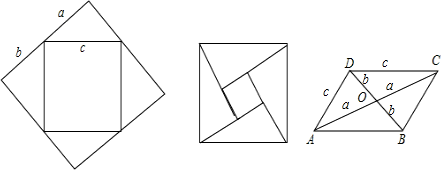
（2）若沿两条对角线把菱形剪开，分成四个三角形，利用这四个三角形可拼成一个可以证明勾股定理的图形．请你画出示意图，并证明勾股定理．
（3）若a=4，b=3，求
①菱形的边长和菱形的面积．（直接写出结论）
②求菱形的高．（直接写出结论）

Answer 1

解：（1）∵四边形ABCD是菱形，
∴对角线AC和BD互相垂直平分．
（2）拼法一：如图，
由大正方形的面积得．
化简得a²+b²=c²

（2）拼法二：如图，
由小正方形的面积得
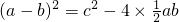
化简得a²+b²=c²

（3）①由上面的结论得
菱形的边长，
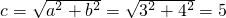菱形的面积=2ab=2×3×4=24，
②根据平行四边形的面积公式可得
菱形的高=
分析：（1）根据菱形的对角线AC和BD互相垂直平分即可直接得出答案．
（2）由2中拼法，拼法一由大正方形的面积得；拼法二由小正方形的面积得，然后化简即可．
（3）①由上面的结论得菱形的边长，然后即可求出面积，②根据平行四边形的面积公式可得菱形的高．
点评：此题主要考查学生对菱形的性质和勾股定理的证明等知识点的理解和掌握．此题中的第（2）问有一定的拔高难度，要求学生具备一定的空间想象能力，因此属于难题．