题目内容
一艘渔船从港口A出发，以20海里/小时的速度向正南方向行驶，行驶一段时间后又折向正东方向，此时一艘快艇也从港口A出发以| 100 | 3 |
（1）画出渔船和快艇行驶的路线图；
（2）快艇用了几小时追上渔船？
分析：（1）根据题意所述，即可画出渔船和快艇行驶的路线图；
（2）设快艇用x小时追上渔船，然后根据勾股定理即可求出x的值．
（2）设快艇用x小时追上渔船，然后根据勾股定理即可求出x的值．
解答：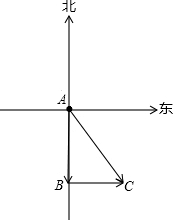
解：（1）渔船和快艇行驶的路线图如下图所示：
渔船的路线图为：A→B→C；快艇的路线图为：A→C．
（2）设快艇用x小时追上渔船，
则AB=20（7-x），BC=20x，AC=
x，
在Rt△ABC中，根据勾股定理得：AC2=BC2+AB2，
代入各值得：（
x）2=（20x）2+[20（7-x）]2，
解得：x=3．
答：快艇用了3小时追上渔船．
解：（1）渔船和快艇行驶的路线图如下图所示：渔船的路线图为：A→B→C；快艇的路线图为：A→C．
（2）设快艇用x小时追上渔船，
则AB=20（7-x），BC=20x，AC=
| 100 |
| 3 |
在Rt△ABC中，根据勾股定理得：AC2=BC2+AB2，
代入各值得：（
| 100 |
| 3 |
解得：x=3．
答：快艇用了3小时追上渔船．
点评：本题考查勾股定理的实际应用，解题关键是读懂题意，然后准确画出渔船和快艇行驶的路线图，再利用勾股定理求解．
练习册系列答案
智慧小复习系列答案
相关题目
近期由于南海争端频发，我国的渔船经常受到一些干扰，有关部门决定派遣渔政执法船护渔．如图，港口B位于港口O正东方向120km处，小岛C位于港口O南偏东60°的方向．一队渔船从港口O出发，以20km/h的速度沿南偏东30°的OA方向驶离港口O．同时一艘渔政执法船从港口B出发，以60km/h的速度沿南偏西30°的方向驶向小岛C，并要在小岛C上停留1小时补给物资，然后按原来的速度向渔船编队驶去．
海里/小时的速度向渔船追去，并在最短时间内追上了渔船，当快艇追上渔船时，渔船共行驶了7小时．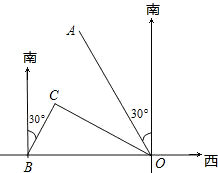
近期由于南海争端频发，我国的渔船经常受到一些干扰，有关部门决定派遣渔政执法船护渔．如图，港口B位于港口O正东方向120km处，小岛C位于港口O南偏东60°的方向．一队渔船从港口O出发，以20km/h的速度沿南偏东30°的OA方向驶离港口O．同时一艘渔政执法船从港口B出发，以60km/h的速度沿南偏西30°的方向驶向小岛C，并要在小岛C上停留1小时补给物资，然后按原来的速度向渔船编队驶去．
海里/小时的速度向渔船追去，并在最短时间内追上了渔船，当快艇追上渔船时，渔船共行驶了7小时．