题目内容
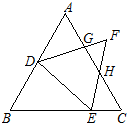 23、如图,△ABC、△ABC都是等边三角形,点D、E分别在AB、BC上.图中有与△DBE相似的三角形吗?请说明理由.
23、如图,△ABC、△ABC都是等边三角形,点D、E分别在AB、BC上.图中有与△DBE相似的三角形吗?请说明理由.分析:首先由△ABC、△DEF都是等边三角形,即可得∠A=∠B=∠C=∠FDE=∠DEF=∠F=60°,∠ADG+∠BDE=120°,∠BDE+∠DEB=120°,即可得∠ADG=∠BED,根据有两角对应相等的三角形相似,即可证得△BDE∽△AGD,同理可证得△BDE∽△CEH,又易证得△CEH∽△FGH,即可求得答案.
解答:解:图中有与△DBE相似的三角形有:△GAD,△ECH,△GFH.
理由:∵△ABC、△DEF都是等边三角形,
∴∠A=∠B=∠C=∠FDE=∠DEF=∠EFD=60°,
∴∠ADG+∠BDE=120°,∠BDE+∠DEB=120°,
∴∠ADG=∠BED,
∴△BDE∽△AGD,
同理:△BDE∽△CEH,
∵∠GHF=∠CHE,∠C=∠F=60°,
∴△CEH∽△FGH,
∴△BDE∽△FGH,
∴图中有与△DBE相似的三角形有:△GAD,△ECH,△GFH.
理由:∵△ABC、△DEF都是等边三角形,
∴∠A=∠B=∠C=∠FDE=∠DEF=∠EFD=60°,
∴∠ADG+∠BDE=120°,∠BDE+∠DEB=120°,
∴∠ADG=∠BED,
∴△BDE∽△AGD,
同理:△BDE∽△CEH,
∵∠GHF=∠CHE,∠C=∠F=60°,
∴△CEH∽△FGH,
∴△BDE∽△FGH,
∴图中有与△DBE相似的三角形有:△GAD,△ECH,△GFH.
点评:此题考查了相似三角形的判定与等边三角形的性质.此题难度适中,解题的关键是掌握有两角对应相等的三角形相似定理的应用与数形结合思想的应用.

练习册系列答案
相关题目
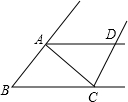 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
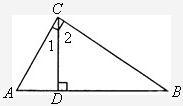
 ,且CB=CE.
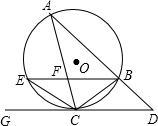
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.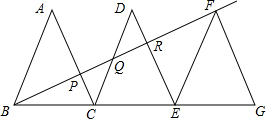 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且