题目内容
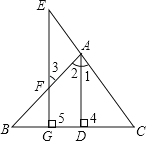
【题目】已知：如图，AD⊥BC于D，EG⊥BC与G，∠E=∠3，试问：AD是∠BAC的平分线吗？若是，请说明理由．
解答：是，理由如下：
∵AD⊥BC，EG⊥BC（已知）
∴∠4=∠5=90°（垂直的定义）
∴AD∥EG
∴∠1=∠E
∠2=∠3
∵∠E=∠3（已知）
∴ =
∴AD是∠BAC的平分线（角平分线的定义）．
【答案】同位角相等，两直线平行，两直线平行，同位角相等，两直线平行，内错角相等，∠1，∠2
【解析】解：是．
∵AD⊥BC，EG⊥BC（已知）
∴∠4=∠5=90°（垂直的定义）
∴AD∥EG，（同位角相等，两直线平行）
∴∠1=∠E，（两直线平行，同位角相等）
∠2=∠3．（两直线平行，内错角相等）
∵∠E=∠3，（已知）
∴∠1=∠2，
∴AD是∠BAC的平分线（角平分线的定义）．
故答案为：同位角相等，两直线平行，两直线平行，同位角相等，两直线平行，内错角相等，∠1，∠2．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
