题目内容
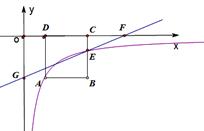
如图,一次函数y=ax+b(b≠0),二次函数y=ax2+bx+c和反比例函数y=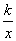 (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是………………………………………………………………………………【 】
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是………………………………………………………………………………【 】
A.b=2a+k B.a=b+k C.a>b>0 D.a>k>0

D 解析:对于选项A:∵点A(﹣2,0)在抛物线上,∴将A点坐标代入抛物线解析式得4a-2b=0,∴b=2a,又∵k≠0,∴b≠2a+k,∴选项A错误;对于选项B:由抛物线可知,a>0,由选项A知b=2a,∴b>a,由双曲线知k>0,∴a<b+k,∴选项B错误;对于选项C:由选项A知b=2a,∴a-b=a-2a=﹣a<0,∴a<b,∴选项C错误;对于选项D:由选项A知b=2a,∴抛物线的对称轴为直线x=﹣1,顶点坐标为(﹣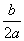 ,
,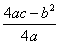 ),又抛物线过点(0,0),∴顶点坐标为(﹣1,﹣a),抛物线的对称轴直线x=﹣1与反比例函数图象的交点为(﹣1,﹣k),从图象可看出当x=﹣1时,点(﹣1,﹣k)在点(﹣1,﹣a)的上方,∴﹣k>﹣a,∴k<a,∴a>k>0.∴选项D正确.
),又抛物线过点(0,0),∴顶点坐标为(﹣1,﹣a),抛物线的对称轴直线x=﹣1与反比例函数图象的交点为(﹣1,﹣k),从图象可看出当x=﹣1时,点(﹣1,﹣k)在点(﹣1,﹣a)的上方,∴﹣k>﹣a,∴k<a,∴a>k>0.∴选项D正确.

 阅读快车系列答案
阅读快车系列答案某超市销售多种颜色的服装,其中平均每天销售红、黄、蓝、白4种颜色运动服的数量如下表,由此绘制的不完整的扇形统计图如下图.2-1-c-n-j-y
| 服装颜色 | 红 | 黄 | 蓝 | 白 | 合计 |
| 数量/件 | 20 | n | 40 | 1.5n | m |
| 所对扇形的圆心角 |
| 90° | 360° |

(1)求表中m,n,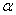 的值,并将扇形统计图补充完整;
的值,并将扇形统计图补充完整;
(2)为吸引更多的顾客,超市将上述扇形统计图制成一个可自由转动的转盘,并规定:顾客在本超市购买商品金额达到一定的数目,就获得一次转动转盘的机会.如果转盘停止后,指针指向红色服装区域、黄色服装区域,可分别获得60元、20元的购物券,求顾客每转动一次转盘获得购物券金额的平均数.
 ,它们运动的速度都是1cm/秒.设P、Q同发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:AD=BE=5;cos∠ABE=
,它们运动的速度都是1cm/秒.设P、Q同发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:AD=BE=5;cos∠ABE=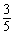 ;当0<t≤5时,y=
;当0<t≤5时,y=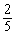 t2;当t=
t2;当t=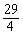 秒时,△ABE∽△QBP;其中正确的结论是_ __(填序号).
秒时,△ABE∽△QBP;其中正确的结论是_ __(填序号). 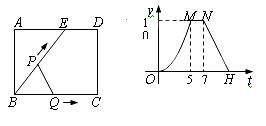
 AB落在x轴的负半轴上的平面直角坐标系,则点C的坐标为( )
AB落在x轴的负半轴上的平面直角坐标系,则点C的坐标为( )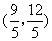 或
或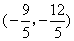 B.
B.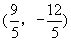
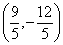 D.
D. 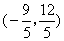 或
或 x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,求直线AM的解析式。
x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,求直线AM的解析式。
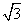 ),则D点的坐标为…………………………………【 】
),则D点的坐标为…………………………………【 】
 的解是
的解是 ,求(a+b)2-(a-b)(a+b)的值.
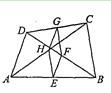
,求(a+b)2-(a-b)(a+b)的值.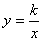 (k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n,
(k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n, ),过点E的直线
),过点E的直线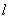 交x轴
交x轴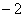 ),则点F的坐标是 .
),则点F的坐标是 .