题目内容
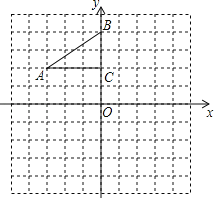
【题目】我们规定:有一组邻边相等,且这组邻边的夹角为![]() 的凸四边形叫做“准筝形”。如图1,四边形ABCD中,若AB=AD,∠A=
的凸四边形叫做“准筝形”。如图1,四边形ABCD中,若AB=AD,∠A=![]() ,则四边形ABCD是“准筝形”。
,则四边形ABCD是“准筝形”。
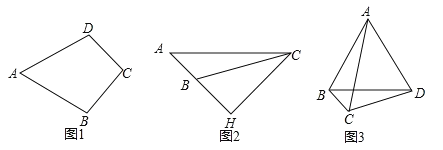
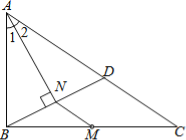
(1)如图2,CH是△ABC的高线,∠A=![]() ,∠ABC=
,∠ABC=![]() ,AB=2.求CH;
,AB=2.求CH;
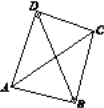
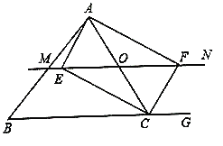
(2) 如图3,四边形ABCD中,BC=2,CD=4,AC=6,∠BCD=![]() ,且AD=BD,试判断四边形ABCD是不是“准筝形”,并说明理由。
,且AD=BD,试判断四边形ABCD是不是“准筝形”,并说明理由。
小红是这样思考的:延长BC至点E,使CE=CD=4,连结DE,则△DCE是等边三角形,再说明△ACD![]() △BED就可以了。请根据小红的思考完成本小题。
△BED就可以了。请根据小红的思考完成本小题。
(3) 在(1)条件下,设D是△ABC所在平面内一点,当四边形ABCD是“准筝形”时,请直接写出四边形ABCD的面积;
【答案】(1)![]() (2)四边形ABCD是“准筝形”,理由见解析;(3)
(2)四边形ABCD是“准筝形”,理由见解析;(3)![]()
【解析】
(1)设BH=x,根据∠ABC=![]() 表示出CH,在根据∠A=
表示出CH,在根据∠A=![]() 列出方程求解即可;(2)延长BC至点E,使CE=CD=4,连结DE,则△DCE是等边三角形,再证明△ACD≌△BED得到△ABD是等边三角形,即可证明四边形ABCD是“准筝形”;(3)在(1)条件下,D是△ABC所在平面内一点,当四边形ABCD是“准筝形”时,分情况讨论①AB=AD=2,∠BAD=60°,②BC=BD=2
列出方程求解即可;(2)延长BC至点E,使CE=CD=4,连结DE,则△DCE是等边三角形,再证明△ACD≌△BED得到△ABD是等边三角形,即可证明四边形ABCD是“准筝形”;(3)在(1)条件下,D是△ABC所在平面内一点,当四边形ABCD是“准筝形”时,分情况讨论①AB=AD=2,∠BAD=60°,②BC=BD=2![]() +2,∠BCD=60°,③AD=CD=AC=
+2,∠BCD=60°,③AD=CD=AC=![]() HC=3
HC=3![]() +
+![]() ,∠ADC=60°,分别求出四边形ABCD的面积即可.
,∠ADC=60°,分别求出四边形ABCD的面积即可.
(1)设BH=x,
∵∠ABC=120°,CH是△ABC的高线,
∴∠BCH=30°,
∴HC=![]() ,
,
∵∠A=45°,
∴HA=HC,
∵AB=2,
∴![]() =2+x,
=2+x,
解得:x=![]() +1,
+1,
∴HC=![]() =3+
=3+![]() ;
;
(2)四边形ABCD是“准筝形”,
理由:如图所示,延长BC至点E,使CE=CD=4,连结DE,
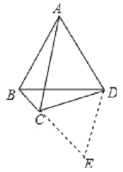
∵∠BCD=120°,
∴∠DCE=60°,
∴△DCE是等边三角形,
∴ED=CD=4,∠CDE=60°,
∵BC=2,CE=CD=4,AC=6,
∴AC=EB,
在△ACD和△BED中,
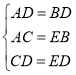
∴△ACD≌△BED(SSS),
∴∠ADC=∠BDE,
∴∠ADB=∠CDE=60°,
∴△ABD是等边三角形,
∴AB=AD,∠BAD=60°,
∴四边形ABCD是“准筝形”;
(3在(1)条件下,D是△ABC所在平面内一点,当四边形ABCD是“准筝形”时,分情况讨论,分别求出四边形ABCD的面积:
①如下图AB=AD=2,∠BAD=60°,
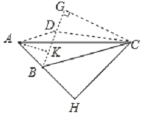
作CG垂直BD的延长线于点G,则BD=2,
易得:∠CBG=60°=∠CBH,
在△CBG和△CBH中
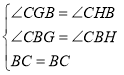
∴△CBG≌△CBH(AAS),
∴GC=HC=3+![]() ,
,
作AK⊥BD于K,则易得:AK=![]() ,
,
∴S△ABD=![]() ×2×
×2×![]() =
=![]() ,S△CBD=
,S△CBD=![]() ×2×(3+
×2×(3+![]() )=3+
)=3+![]() ,
,
∴四边形ABCD的面积=3+2![]() ;
;
②如下图BC=BD=2![]() +2,∠BCD=60°,
+2,∠BCD=60°,
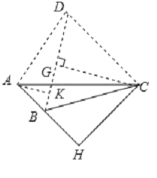
作CG垂直BD的延长线于点G,则BD=2![]() +2,
+2,
易得:CG=3+![]() ,AK=
,AK=![]() ,
,
∴S△BCD=![]() ×(3+
×(3+![]() )(2+2
)(2+2![]() )=4
)=4![]() +6,
+6,
S△ABD=![]() ×
×![]() ×(2+2
×(2+2![]() )=3+
)=3+![]() ,
,
∴四边形ABCD的面积=9+5![]() ;
;
③如下图AD=CD=AC=![]() HC=3
HC=3![]() +
+![]() ,∠ADC=60°,
,∠ADC=60°,
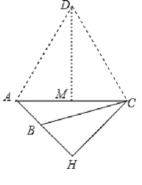
作DM⊥AC于M,
易得:DM=![]() (3
(3![]() +
+![]() )=
)=![]() (
(![]() +
+![]() ),
),
∴S△ABC=![]() ×2×(3+
×2×(3+![]() )=3+
)=3+![]() ,
,
S△ADC=![]() ×(3
×(3![]() +
+![]() )×
)×![]() (
(![]() +
+![]() )=6
)=6![]() +9,
+9,
∴四边形ABCD的面积=12+7![]() ,
,
综上所述,四边形ABCD的面积为![]()

 ABC考王全优卷系列答案
ABC考王全优卷系列答案