Question

在平面直角坐标系中，抛物线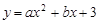与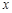轴的两个交点分别为A（-3，0）、B（1，0），过顶点C作CH⊥x轴于点H.
（1）求抛物线的解析式和顶点坐标；
（2）在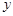轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标.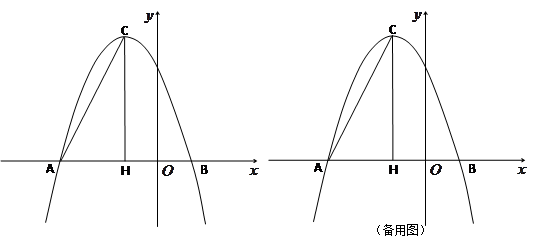

Answer 1

解：（1）由题意，得
解得，
抛物线的解析式为y=-x²-2x+3
顶点C的坐标为（-1，4）
（2）假设在y轴上存在满足条件的点D, 过点C作CE⊥y轴于点E.

由∠CDA=90°得，∠1+∠2=90°. 又∠2+∠3=90°，
∴∠3=∠1. 又∵∠CED=∠DOA =90°，
∴△CED∽△DOA，
∴.
设D（0，c），则. 
变形得，解之得.
综合上述：在y轴上存在点D（0，3）或（0，1），
使△ACD是以AC为斜边的直角三角形. 
（3）①若点P在对称轴右侧（如图①），

只能是△PCQ∽△CAH，得∠QCP=∠CAH.
延长CP交x轴于M，∴AM=CM， ∴AM²=CM².
设M（m，0），则( m+3)²=4²+(m+1)²，∴m=2，即M（2，0）.
设直线CM的解析式为y=k₁x+b₁，
则， 解之得，.
∴直线CM的解析式.
，
解得， (舍去).
.           
∴.
②若点P在对称轴左侧（如图②），

只能是△PCQ∽△ACH，得∠PCQ=∠ACH.
过A作CA的垂线交PC于点F，作FN⊥x轴于点N.
由△CFA∽△CAH得，
由△FNA∽△AHC得.
∴, 点F坐标为（-5,1）.
设直线CF的解析式为y=k₂x+b₂，则，解之得.
∴直线CF的解析式. 
，
解得， (舍去).
∴.   
∴满足条件的点P坐标为或 

解析