Question

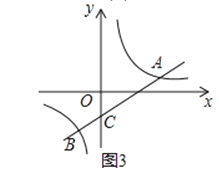
【题目】在第一象限内，点P（2，3），M（a，2）是双曲线y=（k≠0）上的两点，PA⊥x轴于点A，MB⊥x轴于点B，PA与OM交于点C，则△OAC的面积为

Answer 1

【答案】
【解析】∵点P（2，3）在双曲线y=（k≠0）上，
∴k=2×3=6，
∴y=，
当y=2时，x=3，即M（3，2）．
∴直线OM的解析式为y=x，
当x=2时，y=，即C（2，）．
∴△OAC的面积=×2×=．
故答案为：．
由于点P（2，3）在双曲线y=（k≠0）上，首先利用待定系数法求出k的值，得到反比例函数的解析式，把y=2代入，求出a的值，得到点M的坐标，然后利用待定系数法求出直线OM的解析式，把x=2代入，求出对应的y值即为点C的纵坐标，最后根据三角形的面积公式求出△OAC的面积．