题目内容
（2013•道外区一模）线段AB=3，分别以A、B为圆心作⊙A，⊙B，其中⊙A的半径为1，若⊙B与⊙A内切，则⊙B的半径长为（ ）
分析：根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可求解．两圆的位置关系有：相离（d＞R+r）、相切（外切：d=R+r或内切：d=R-r）、相交（R-r＜d＜R+r）．
解答：解：设⊙B的半径长为r，
∵⊙A的半径为1，⊙B与⊙A内切，AB=3，
∴AB=r-1=3，
解得：r=4．
故选D．
∵⊙A的半径为1，⊙B与⊙A内切，AB=3，
∴AB=r-1=3，
解得：r=4．
故选D．
点评：本题主要考查两圆的位置关系．
两圆的位置关系有：相离（d＞R+r）、相切（外切：d=R+r或内切：d=R-r）、相交（R-r＜d＜R+r）．
两圆的位置关系有：相离（d＞R+r）、相切（外切：d=R+r或内切：d=R-r）、相交（R-r＜d＜R+r）．
练习册系列答案
相关题目
（2013•道外区一模）如图，在△ABC中，AB=AC，∠ABC=40°，把△ABC绕点A逆时针旋转20°得到△ADE（点D与点B是对应点，点E与点C是对应点），连接BD，则∠DBC的度数为（ ）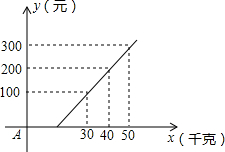
（2013•道外区一模）如图所示，是某航空公司托运行李的费用y（元）与行李重量x（千克）的关系图象，由图中可知，乘客可以免费托运行李的最大重量为（ ）