题目内容
如图，某城市公园的雕塑是由3个直径为1m的圆两两相垒立在水平的地面上，则雕塑的最高点到地面的距离为________．
（1+
）m
分析：三个等圆的圆心分别为A、B、C，过A作AD⊥BC于D，交地面于E，交⊙A于F，根据相切两圆的性质得到AB=BC=AC=1m，再利用等边三角形的性质可得到AD=BC，然后由
AF+AD+DE计算出雕塑的最高点到地面的距离．
解答：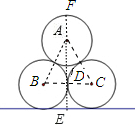
解：如图，三个等圆的圆心分别为A、B、C，过A作AD⊥BC于D，交地面于E，交⊙A于F，
则△ABC为等边三角形，且边长为1m，
∴AD=BC=，
∴EF=1+，
所以雕塑的最高点到地面的距离为（1+）m．
故答案为（1+）m．
点评：本题考查了相切两圆的性质：相切两圆的圆心距等于两圆半径之和．也考查了等边三角形的性质．
）m分析：三个等圆的圆心分别为A、B、C，过A作AD⊥BC于D，交地面于E，交⊙A于F，根据相切两圆的性质得到AB=BC=AC=1m，再利用等边三角形的性质可得到AD=
BC，然后由AF+AD+DE计算出雕塑的最高点到地面的距离．
解答：
解：如图，三个等圆的圆心分别为A、B、C，过A作AD⊥BC于D，交地面于E，交⊙A于F，则△ABC为等边三角形，且边长为1m，
∴AD=
BC=，∴EF=1+
，所以雕塑的最高点到地面的距离为（1+
）m．故答案为（1+
）m．点评：本题考查了相切两圆的性质：相切两圆的圆心距等于两圆半径之和．也考查了等边三角形的性质．
练习册系列答案
相关题目
如图，某城市公园的雕塑是由3个直径为1m的圆两两相垒立在水平的地面上，则雕塑的最高点到地面的距离为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，某城市公园的雕塑是由3个直径为1m的圆两两相垒立在水平的地面上，则雕塑的最高点到地面的距离为
