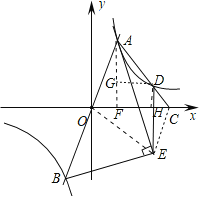
题目内容
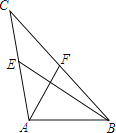
【题目】如图,过原点的直线与反比例函数![]() 的图象交于
的图象交于![]() 两点,点
两点,点![]() 在第一象限。点
在第一象限。点![]() 在
在![]() 轴正半轴上,连结
轴正半轴上,连结![]() 交反比例函数图象于点
交反比例函数图象于点![]() 。
。![]() 为
为![]() 的平分线,过点
的平分线,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,连结
,连结![]() 。若
。若![]() ,
,![]() 的面积为6,则
的面积为6,则![]() 的值为________。
的值为________。
【答案】![]()
【解析】
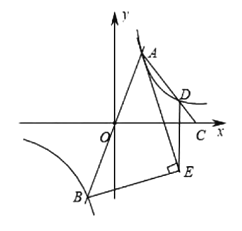
连接OE,CE,过点A作AF⊥x轴,过点D作DH⊥x轴,过点D作DG⊥AF;由AB经过原点,则A与B关于原点对称,再由BE⊥AE,AE为∠BAC的平分线,可得AD∥OE,进而可得S△ACE=S△AOC;设点A(m,![]() ),由已知条件AC=3DC,DH∥AF,可得3DH=AF,则点D(3m,
),由已知条件AC=3DC,DH∥AF,可得3DH=AF,则点D(3m,![]() ),证明△DHC∽△AGD,得到S△HDC=
),证明△DHC∽△AGD,得到S△HDC=![]() S△ADG,所以S△AOC=S△AOF+S梯形AFHD+S△HDC=
S△ADG,所以S△AOC=S△AOF+S梯形AFHD+S△HDC=![]() k+
k+![]() +
+![]() =9;即可求解;
=9;即可求解;
解:
连接OE,CE,过点A作AF⊥x轴,过点D作DH⊥x轴,过点D作DG⊥AF,
∵过原点的直线与反比例函数y=![]() (k>0)的图象交于A,B两点,
(k>0)的图象交于A,B两点,
∴A与B关于原点对称,
∴O是AB的中点,
∵BE⊥AE,
∴OE=OA,
∴∠OAE=∠AEO,
∵AE为∠BAC的平分线,
∴∠DAE=∠AEO,
∴AD∥OE,
∴S△ACE=S△AOC,
∵AC=3DC,△ADE的面积为6,
∴S△ACE=S△AOC=9,
设点A(m,![]() ),
),
∵AC=3DC,DH∥AF,
∴3DH=AF,
∴D(3m,![]() ),
),
∵CH∥GD,AG∥DH,
∴△DHC∽△AGD,
∴S△HDC=![]() S△ADG,
S△ADG,
∵S△AOC=S△AOF+S梯形AFHD+S△HDC=![]() k+
k+![]() ×(DH+AF)×FH+S△HDC=
×(DH+AF)×FH+S△HDC=![]() k+
k+![]() ×
×![]() ×2m+
×2m+
![]() ×
×![]() ×
×![]() ×2m=
×2m=![]() k+
k+![]() +
+![]() =9,
=9,
∴2k=9,
∴k=![]() ;
;
故答案为![]() .
.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目