Question

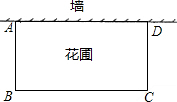张大爷要围成一个矩形花圃．花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成．围成的花圃是如图所示的矩形ABCD．设AB边的长为x米．矩形ABCD的面积为S平方米．
（1）求S与x之间的函数关系式（不要求写出自变量x的取值范围）；
（2）当x为何值时，S有最大值并求出最大值．
（参考公式：二次函数y=ax²+bx+c（a≠0），当x=-

b

2a

时，y_{最大（小）值}=

4ac-b2

4a

）

Answer 1

分析：在题目已设自变量的基础上，表示矩形的长，宽；用面积公式列出二次函数，用二次函数的性质求最大值．

解答：解：（1）由题意，得S=AB•BC=x（32-2x），
∴S=-2x²+32x．

（2）∵a=-2＜0，
∴S有最大值．
∴x=-

b

2a

=-

32

2×(-2)

=8时，有S_最大=

4ac-b2

4a

=

-322

4×(-2)

=128．
∴x=8时，S有最大值，最大值是128平方米．

点评：求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法，当二次项系数a的绝对值是较小的整数时，用配方法较好，如y=-x²-2x+5，y=3x²-6x+1等用配方法求解比用公式法简便．