��Ŀ����
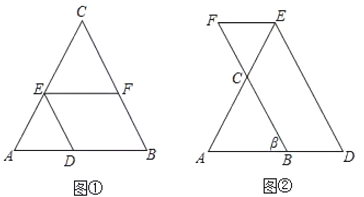
����Ŀ���������ڽǷֱ������ǶԽǵ�һ����ı��ν�����Խ��ı��Σ�
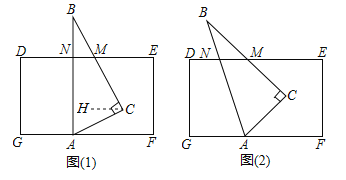
��1����ͼ1���ڰ�Խ��ı���ABCD�У���B�� ![]() ��D����C��
��D����C�� ![]() ��A�����B���C�Ķ���֮�ͣ�
��A�����B���C�Ķ���֮�ͣ�
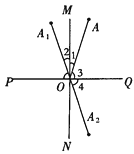
��2����ͼ2����ǡ�ABC�ڽ��ڡ�O������AB�ϴ���һ��D��ʹ��BD��BO����OBA��ƽ���߽�OA�ڵ�E������DE���ӳ���AC�ڵ�F����AFE��2��EAF��
��֤���ı���DBCF�ǰ�Խ��ı��Σ�
��3����ͼ3���ڣ�2���������£�����D��DG��OB�ڵ�H����BC�ڵ�G����DH��BGʱ�����BGH���ABC�����֮�ȣ�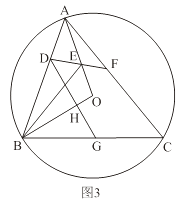
���𰸡�
��1��
�⣺�ڰ�Խ��ı���ABCD�У���B=![]() ��D����C=
��D����C=![]() ��A.
��A.
�ߡ�A+��B+��C+��D=360�㣬
��3��B+3��C=360��.
���B+��C=120��.
����B���C�Ķ���֮��120��.
��2��
֤�����ڡ�BED�͡�BEO�У�
 .
.
���BED�ա�BEO��SAS��.
���BDE=��BOE.
�֡ߡ�BCF=![]() ��BOE.
��BOE.
���BCF=![]() ��BDE.
��BDE.
����ͼ������OC.
���EAF=![]() .���AFE=2��EAF=2
.���AFE=2��EAF=2![]() .
.
���EFC=180��-��AFE=180��-2![]() .
.
��OA=OC,
���OAC=��OCA=![]() .
.
���AOC=180��-��OAC-��OCA=180��-2![]() .
.
���ABC=![]() ��AOC=
��AOC=![]() ��EFC.
��EFC.
���ı���DBCF�ǰ�Խ��ı���.

��3��
�⣺����ͼ��������OM��BC�ڵ�M.
���ı���DBCF�ǰ�Խ��ı��Σ�
���ABC+��ACB=120��.
���BAC=60��.
���BOC=2��BAC=120��.
��OB=OC
���OBC=��OCB=30��.
��BC=2BM=![]() BO=
BO=![]() BD.
BD.
��DG��OB,
���HGB=��BAC=60��.
�ߡ�DBG=��CBA,
���DBG![]() ��CBA.
��CBA.
��![]() =
=![]() 2=
2=![]() .
.
��DH=BG,BG=2HG.
��DG=3HG.
��![]() =
=![]()
��![]() =
=![]() .
.

����������1���ڰ�Խ��ı���ABCD�У���B=![]() ��D����C=
��D����C=![]() ��A�������ı��ε��ڽǺ�Ϊ360�㣬�ó���B���C�Ķ���֮��.
��A�������ı��ε��ڽǺ�Ϊ360�㣬�ó���B���C�Ķ���֮��.
��2����ͼ����OC������������֤��BED�ա�BEO���ٸ���ȫ�������ε����ʵó���BCF=![]() ��BOE=
��BOE=![]() ��BDE�����EAF=
��BDE�����EAF=![]() .���AFE=2��EAF=2
.���AFE=2��EAF=2![]() ��EFC=180��-��AFE=180��-2
�ó���EFC=180��-��AFE=180��-2![]() ���ٸ���OA=OC�ó���OAC=��OCA=
���ٸ���OA=OC�ó���OAC=��OCA=![]() �� �����������ڽǺ͵ó���AOC=180��-��OAC-��OCA=180��-2
�� �����������ڽǺ͵ó���AOC=180��-��OAC-��OCA=180��-2![]() ���Ӷ���֤.
���Ӷ���֤.
��3������ͼ��������OM��BC�ڵ�M�����ı���DBCF�ǰ�Խ��ı��Σ��ó���ABC+��ACB=120�㣬��BAC=60��.��BOC=2��BAC=120�㣻����OB=OC���ó���OBC=��OCB=30��.BC=2BM=![]() BO=
BO=![]() BD�����ݡ�DBG����CBA�ó���.
BD�����ݡ�DBG����CBA�ó���.
�����㾫�������������ε��ڽǺ���Ǻ͵��������ε������ǽ����ĸ�������Ҫ֪�������ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ����������ε���������ȣ���ƣ��ȱ߶ԵȽǣ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��Сӱ��С����λͬѧ��ѧϰ�����ʡ�ʱ����Ͷ�����ӣ��ʵؾ��ȵ������壩���飬���ǹ�����60�����飬����Ľ�����£�
���ϵĵ��� | 1 | 2 | 3 | 4 | 5 | 6 |
���ֵĴ��� | 7 | 9 | 6 | 8 | 20 | 10 |
��1�����㡰3�㳯�ϡ���Ƶ�ʺ͡�5�㳯�ϡ���Ƶ��.
��2��Сӱ˵���������������飬һ�������г���5�㳯�ϵĸ������С��˵�������Ͷ��600�Σ���ô����6�㳯�ϵĴ���������100�Ρ�.Сӱ��С���˵����ȷ��Ϊʲô��