题目内容
已知一次函数 的图像和二次函数
的图像和二次函数 的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5.
的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5. 
(1)求这个二次函数的解析式;
(2)将此二次函数图像的顶点记作点P,求△ABP的面积;
(3)已知点C、D在射线AB上,且D点的横坐标比C点的横坐标大2,点E、F在这个二次函数图像上,且CE、DF与y轴平行,当
 ∥
∥ 时,求C点坐标.
时,求C点坐标.
(1)A点坐标为(0,1)
将 代入
代入 ,得
,得
∴B点坐标为(4,5)
将A、B两点坐标代入
解得
∴二次函数解析式为
(2)P点坐标为( ,
, )
)
抛物线对称轴与直线AB的交点记作点G,则点G( ,
, )
)
∴PG= ,
,
∴ .
.
(3)设C点横坐标为
则C点坐标为 ,D点坐标为
,D点坐标为 ,
,
E点坐标为 ,F点坐标为
,F点坐标为 ,
,
由题意,得 CE= ,DF=
,DF= ,
,
∵且CE、DF与y轴平行,∴CE∥DF,又∵ ∥
∥ ,
,
∴四边形 是平行四边形,∴
是平行四边形,∴ ,
,
∴ ,解得
,解得 ,
, (舍),
(舍),
∴C点坐标为( ,
, ).解析:
).解析:
二次函数的综合运用
将
 代入
代入 ,得
,得
∴B点坐标为(4,5)
将A、B两点坐标代入

解得

∴二次函数解析式为

(2)P点坐标为(
 ,
, )
)抛物线对称轴与直线AB的交点记作点G,则点G(
 ,
, )
)∴PG=
 ,
,∴
 .
.(3)设C点横坐标为

则C点坐标为
 ,D点坐标为
,D点坐标为 ,
,E点坐标为
 ,F点坐标为
,F点坐标为 ,
,由题意,得 CE=
 ,DF=
,DF= ,
,∵且CE、DF与y轴平行,∴CE∥DF,又∵
 ∥
∥ ,
,∴四边形
 是平行四边形,∴
是平行四边形,∴ ,
,∴
 ,解得
,解得 ,
, (舍),
(舍),∴C点坐标为(
 ,
, ).解析:
).解析:二次函数的综合运用

练习册系列答案
相关题目
 的图像和二次函数
的图像和二次函数 的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5.
的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5. 
 ∥
∥ 时,求C点坐标.
时,求C点坐标. 的图像和二次函数
的图像和二次函数 的图像都经过
的图像都经过 、
、 两点,且点
两点,且点 轴上,
轴上,
 ,求△
,求△ 的面积.
的面积. 的图像和二次函数
的图像和二次函数 的图像都经过
的图像都经过 、
、 两点,且点
两点,且点 轴上,
轴上,
 ,求△
,求△ 的面积.
的面积. 的图像和二次函数
的图像和二次函数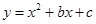 的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5.
的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5. 
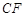 ∥
∥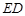 时,求C点坐标.
时,求C点坐标.