题目内容
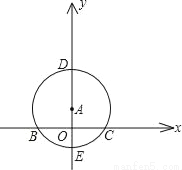
已知:如图,点A在y轴上,⊙A与x轴交于B、C两点,与y轴交于点D(0,3)和点E(0,﹣1)
(1)求经过B、E、C三点的二次函数的解析式;
(2)若经过第一、二、三象限的一动直线切⊙A于点P(s,t),与x轴交于点M,连接PA并延长与⊙A交于点Q,设Q点的纵坐标为y,求y关于t的函数关系式,并观察图形写出自变量t的取值范围;
(3)在(2)的条件下,当y=0时,求切线PM的解析式,并借助函数图象,求出(1)中抛物线在切线PM下方的点的横坐标x的取值范围.
练习册系列答案
相关题目
以下图标是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
(1)平均数为320件,中位数是210件,众数是210件;(2)不合理,定210件 【解析】试题分析:(1)根据平均数、中位数和众数的定义即可求得结果; (2)把月销售额320件与大部分员工的工资比较即可判断. (1)平均数件, ∵最中间的数据为210, ∴这组数据的中位数为210件, ∵210是这组数据中出现次数最多的数据, ∴众数为210件; (...

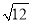 +|
+|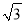 ﹣3|﹣2sin60°﹣(
﹣3|﹣2sin60°﹣(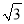 )2+20160.
)2+20160.