题目内容
含30°角的直角三角板ABC中,∠A=30°.将其绕直角顶点C顺时针旋转 角(
角( 且
且 ≠ 90°),得到Rt△
≠ 90°),得到Rt△ ,
, 边与AB所在直线交于点D,过点 D作DE∥
边与AB所在直线交于点D,过点 D作DE∥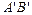 交
交 边于点E,连接BE.
边于点E,连接BE.
(1)如图1,当
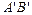 边经过点B时,
边经过点B时, = °;
= °;(2)在三角板旋转的过程中,若∠CBD的度数是∠CBE度数的m倍,猜想m的值并证明你的结论;
(3) 设 BC=1,AD=x,△BDE的面积为S,以点E为圆心,EB为半径作⊙E,当S=

时,求AD的长,并判断此时直线
 与⊙E的位置关系.
与⊙E的位置关系.
(1)60
(2)证明略
(3)直线
 与⊙E相交解析:
与⊙E相交解析:(1)当
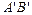 边经过点B时,
边经过点B时, =" 60 " °;………………………… 1分
=" 60 " °;………………………… 1分(2)猜想:①如图8,点D在AB边上时,m=2;
②如图9,点D在AB的延长线上时,m=4.
(阅卷说明:为与后边证明不重复给分,猜想结论不设给分点)
证明:① 当
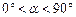 时,点D在AB边上(如图8).
时,点D在AB边上(如图8).
(阅卷说明:①、②两种情况没写
 的取值范围不扣分)
的取值范围不扣分)∵ DE∥
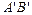 ,
,∴
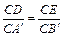 .
.由旋转性质可知,CA =
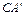 ,CB=
,CB= ,∠ACD=∠BCE.
,∠ACD=∠BCE.∴
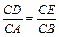 .
. ∴ △CAD∽△CBE. ……………2分
∴ ∠A =∠CBE=30°.
∵ 点D在AB边上,∠CBD=60°,
∴
 ,即 m="2." ………………………………………3分
,即 m="2." ………………………………………3分② 当
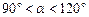 时,点D在AB的延长线上(如图9).
时,点D在AB的延长线上(如图9).
与①同理可得 ∠A =∠CBE=30°.
∵ 点D在AB的延长线上,
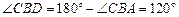 ,
,∴
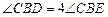 ,即 m="4. " ……………………………………4分
,即 m="4. " ……………………………………4分(阅卷说明:第(2)问用四点共圆方法证明的扣1分.)
(3)解:在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,
∴ AB =" 2" ,
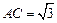 ,
,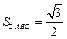 .
.由 △CAD∽△CBE 得
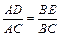 .
.∵ AD=x,
∴
 ,
,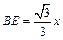 .
.①当点D在AB边上时,AD=x,
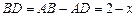 ,∠DBE=90°.
,∠DBE=90°.此时,
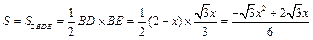 .
.当S =
 时,
时, .
.整理,得
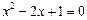 .
.解得
 ,即AD=1.…………………5分
,即AD=1.…………………5分此时D为AB中点,∠DCB=60°,∠BCE=30°=∠CBE.(如图10)

∴ EC = EB.
∵
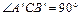 ,点E在
,点E在 边上,
边上,∴ 圆心E到
 的距离EC等于⊙E的半径EB.
的距离EC等于⊙E的半径EB.∴ 直线
 与⊙E相切. …………………………………………………6分
与⊙E相切. …………………………………………………6分②当点D在AB的延长线上时,AD=x,
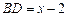 ,∠DBE=90°.(如图9).
,∠DBE=90°.(如图9). .
.当S =
 时,
时,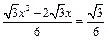 .
.整理,得
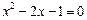 .
.解得
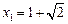 ,
, (负值,舍去).
(负值,舍去). 即
 .……………………………………………………………… 7分
.……………………………………………………………… 7分此时∠BCE=
 ,而
,而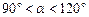 ,∠CBE=30°,
,∠CBE=30°,∴ ∠CBE<∠BCE .
∴ EC<EB,即圆心E到
 的距离EC小于⊙E的半径EB.
的距离EC小于⊙E的半径EB.∴ 直线
 与⊙E相交. ……………………………………………………8分
与⊙E相交. ……………………………………………………8分 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 14、把两个一样大的含30°角的直角三角板按如图的方式拼在一起,其中AC平分∠BAF,AD平分∠EAF,请写出所有的等腰三角形:
14、把两个一样大的含30°角的直角三角板按如图的方式拼在一起,其中AC平分∠BAF,AD平分∠EAF,请写出所有的等腰三角形: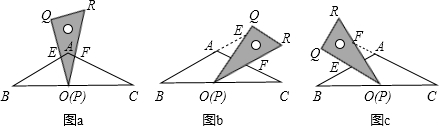
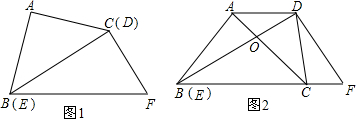

 如图,有一位同学用一个含30°角的直角三角板估测学校的旗杆AB的高度,他将30°角的直角边水平放在1.3米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为15米,则旗杆AB的高度为( )(
如图,有一位同学用一个含30°角的直角三角板估测学校的旗杆AB的高度,他将30°角的直角边水平放在1.3米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为15米,则旗杆AB的高度为( )(