题目内容
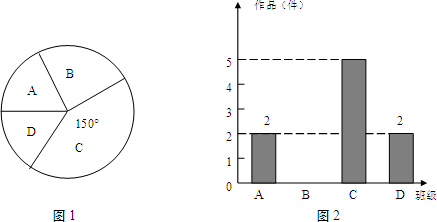
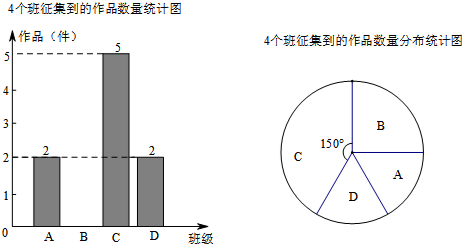
某中学艺术节期间,向全校学生征集书画作品.美术社团从九年级14个班中随机抽取了4个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
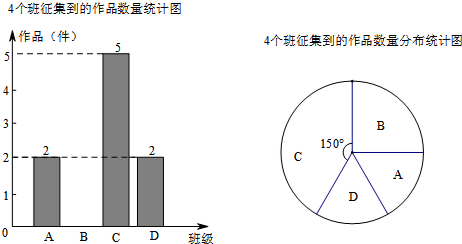
(1)直接回答美术社团所调查的4个班征集到作品共______件,并把图1补充完整;
(2)根据美术社团所调查的四个班征集作品的数量情况,估计全年级共征集到作品的数量为______;
(3)在全年级参展作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生.现在要在其中抽两人去参加学校总结表彰座谈会,用树状图或列表法,求恰好抽中一男生一女生的概率.
解:(1)根据题意得:
调查的4个班征集到作品数为:5÷ =12,
=12,
B班作品的件数为:12-2-5-2=3.
如图:
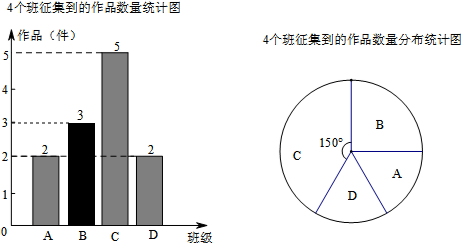
(2)∵美术社团所调查的四个班平均每个班征集作品是:12÷4=3(件),
∴全校共征集到的作品:3×14=42(件);
(3)列表如下:
共有20种机会均等的结果,其中一男生一女生占12种,
∴P(一男生一女生)= ,
,
即恰好抽中一男生一女生的概率为 .
.
故答案为12,42.
分析:(1)根据C班在扇形图中的角度求出所占的份数,再根据C班的人数是5,列式进行计算即可求出作品的总件数,然后减去A、C、D三个班的件数即为B班的件数;
(2)先求出平均每一个班的作品件数,然后乘以班级数14,计算即可得解;
(3)先列表,再根据概率公式进行计算即可得解.
点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.同时考查了概率公式.
调查的4个班征集到作品数为:5÷
 =12,
=12,B班作品的件数为:12-2-5-2=3.
如图:

(2)∵美术社团所调查的四个班平均每个班征集作品是:12÷4=3(件),
∴全校共征集到的作品:3×14=42(件);
(3)列表如下:
| 男1 | 男2 | 男3 | 女1 | 女2 | |
| 男1 | 男1男2 | 男1男3 | 男1女1 | 男1女2 | |
| 男2 | 男2男1 | 男2男3 | 男2女1 | 男2女2 | |
| 男3 | 男3男1 | 男3男2 | 男3女1 | 男3女2 | |
| 女1 | 女1男1 | 女1男2 | 女1男3 | 女1女2 | |
| 女2 | 女2男1 | 女2男2 | 女2男3 | 女2女1 |
∴P(一男生一女生)=
 ,
,即恰好抽中一男生一女生的概率为
 .
.故答案为12,42.
分析:(1)根据C班在扇形图中的角度求出所占的份数,再根据C班的人数是5,列式进行计算即可求出作品的总件数,然后减去A、C、D三个班的件数即为B班的件数;
(2)先求出平均每一个班的作品件数,然后乘以班级数14,计算即可得解;
(3)先列表,再根据概率公式进行计算即可得解.
点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.同时考查了概率公式.

练习册系列答案
相关题目