题目内容
在数列:1,2,3,4,3,4,5,6,5,6,7,8,7,8,9,10…问第2014个数字是 .
考点:规律型:数字的变化类
专题:规律型
分析:把原数据重新排列,第1组数:1,2,3,4,第2组数:3,4,5,6,第3组数:5,6,7,8,则每组数的第1个数为组数的2倍减1,所以第n组数为2n-1,2n,2n+1,2n+2,由于2014=503×4+2,所以第2014个数是第504组的第二个数,于是计算504×2即可.
解答:解:把原数列的排列方式变成:
第1组数:1,2,3,4,
第2组数:3,4,5,6,
第3组数:5,6,7,8
…
第n组数为2n-1,2n,2n+1,2n+2,
因为2014=503×4+2,
所以第2014个数是第504组的第二个数,即504×2=1008.
故答案为1008.
第1组数:1,2,3,4,
第2组数:3,4,5,6,
第3组数:5,6,7,8
…
第n组数为2n-1,2n,2n+1,2n+2,
因为2014=503×4+2,
所以第2014个数是第504组的第二个数,即504×2=1008.
故答案为1008.
点评:本题考查了规律型-数字的变化类:通过特殊数字的变化情况找出其中不变的因素,然后进行推广得到一般的变化规律.

练习册系列答案
相关题目
如果a=
+
,b=
,那么a与b的关系式( )
| 6 |
| 5 |
| 1 | ||||
|
| A、a与b互为相反数 |
| B、a与b互为倒数 |
| C、a>b |
| D、a=b |
 如图,∠B=∠D=90°,BC=DC,∠1=40°,则∠2=
如图,∠B=∠D=90°,BC=DC,∠1=40°,则∠2= 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=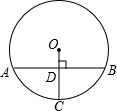 如图,在⊙O中,OC垂直弦AB于点D,交⊙O于点C,若AB=24,半径OC=13,则CD的长是
如图,在⊙O中,OC垂直弦AB于点D,交⊙O于点C,若AB=24,半径OC=13,则CD的长是 已知△ABC与△DEF是全等三角形,试分析△ABC怎样变化才能得到△DEF.
已知△ABC与△DEF是全等三角形,试分析△ABC怎样变化才能得到△DEF.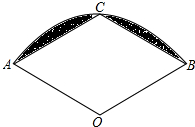 如图,在扇形AOB中,半径OA=1,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是
如图,在扇形AOB中,半径OA=1,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是