Question

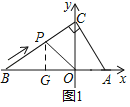
【题目】如图1，在平面直角坐标系中，点A坐标为(2，0)，点B在x轴负半轴上，C在y轴正半轴上，∠ACB＝90°，∠ABC＝30°．

(1)求点B坐标；

(2)如图2，点P从B出发，沿线段BC运动，点P运动速度为每秒2个单位长度，设运动时间为t秒，用含t的式子表示三角形△OBP的面积S；

(3)如图3，在(2)的条件下，点P出发的同时，点Q从O出发，在线段OC上运动，运动速度为每秒2个单位长度，一个点到达终点，另一个点也停止运动．连接PQ，以PQ为一边，在第二象限作等边△PQM，作ME⊥y轴于E，点D为PC中点，作DN⊥BC交y轴于N，若CE＝BP，BC＝4，求N的坐标．

Answer 1

【答案】（1）B(﹣6，0)；（2）S＝3t；（3）N(0，﹣)．

【解析】

(1) 由A(2，0)，可得OA＝2，根据含30°角的直角三角形的性质求出AC 、AB即可解决问题；

(2)如图1，作高线PG，根据直角三角形30度角的性质可得PG的长为t，利用三角形面积公式可得S；

(3)如图2，作辅助线，证明△PCN是等边三角形，再证明△MPC≌△QPN(SAS)，得QN＝CM，∠MCP＝∠QNP＝60°，得到30度的直角△MCE，并求得CM＝QN＝2，根据CE＝BP可得结论．

解：(1)∵A(2，0)，

∴OA＝2，

∵∠ACB＝90°，∠ABC＝30°，

∴∠BAC＝60°，

∴∠ACO＝30°，

∴AC＝2OA=4，

∴AB＝2AC＝8，

∴OB＝8﹣2＝6，

∴B(﹣6，0)．

(2)如图1，过P作PG⊥x轴于G，

由题意得：BP＝2t，

Rt△BPG中，∠B＝30°，

∴PG＝BP＝t，

∴S＝＝×6×t＝3t；

(3)如图2，连接PN、CM．

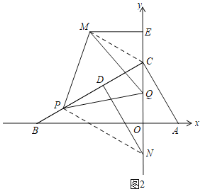
∵BP＝2t，BC＝4，

∴PC＝4﹣2t，

∵D是PC的中点，

∴PD＝CD，

∵DN⊥PC，

∴PN＝CN，

∵∠PCN＝60°，

∴△PCN是等边三角形，

∴PC＝PN＝CN＝4﹣2t，∠NPC＝60°，

∵△PQM是等边三角形，

∴PM＝PQ，∠MPQ＝60°，

∴∠MPQ＝∠CPN＝60°，

∴∠MPC＝∠QPN，

∴△MPC≌△QPN(SAS)，

∴QN＝CM，∠MCP＝∠QNP＝60°，

∵∠PCN＝60°，

∴∠MCE＝60°，

∵OC＝2，OQ＝2t，

∴CQ＝2﹣2t，

∴QN＝CN﹣CQ＝4﹣2t﹣(2﹣2t)＝2，

∴CM＝QN＝2，

Rt△MCE中，∠MCE＝60°，

∴CE＝CM＝，

∵CE＝BP＝2t＝，

∴ON＝QN﹣OQ＝2﹣2t＝2﹣＝，

∴N(0，﹣)．