题目内容
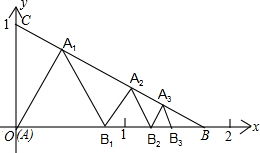 如图所示,已知:点A(0,0),B(
如图所示,已知:点A(0,0),B(| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:图中的各个等边三角形一定相似,求得相似比,即可求解.
解答: 解:如图,过A1作A1D⊥BC于点D.
解:如图,过A1作A1D⊥BC于点D.
设AD=DB1=x
则由△AA1B1∽△B1A2B2,
=
解得x=
所以A2B1B2的边长为
.
同理解得边长依次为
,
…
所以第n个等边三角形的边长等于
.
故选A.
 解:如图,过A1作A1D⊥BC于点D.
解:如图,过A1作A1D⊥BC于点D.设AD=DB1=x
则由△AA1B1∽△B1A2B2,
| ||
| 1 |
| ||
|
解得x=
| ||
| 4 |
所以A2B1B2的边长为
| ||
| 2 |
同理解得边长依次为
| ||
| 4 |
| ||
| 8 |
所以第n个等边三角形的边长等于
| ||
| 2n |
故选A.
点评:本题主要考查了三角形相似的性质,对应边的比相等,正确求得相似比是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
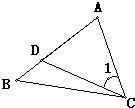 27、如图所示,已知:点D在△ABC的边AB上,连接CD,∠1=∠B,AD=4,AC=5,求BD的长.
27、如图所示,已知:点D在△ABC的边AB上,连接CD,∠1=∠B,AD=4,AC=5,求BD的长.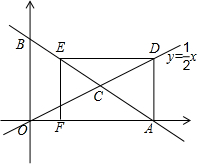 如图所示,已知A点的坐标为(6,0),B是y轴正半轴上的一动点,直线AB交直线
如图所示,已知A点的坐标为(6,0),B是y轴正半轴上的一动点,直线AB交直线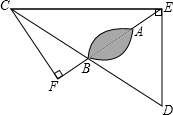 (2013•梧州)海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=8.3海里,DE=30海里,且DE⊥EC,cos∠D=
(2013•梧州)海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=8.3海里,DE=30海里,且DE⊥EC,cos∠D= 如图所示,已知A点的坐标为(0,3),⊙A的半径为1,点B在x轴上.
如图所示,已知A点的坐标为(0,3),⊙A的半径为1,点B在x轴上.