题目内容
已知四边形ABCD是菱形，O是两条对角线的交点，若AB=10，AO=6，则该菱形的面积是________．
96
分析：由四边形ABCD是菱形，根据菱形的性质，可得AC⊥BD，AC=2OA，BD=2OB，又由勾股定理，即可求得OB的长，继而求得AC与BD的长，则可求得该菱形的面积．
解答：∵四边形ABCD是菱形，
∴AC⊥BD，AC=2OA，BD=2OB，
∵AB=10，AO=6，
在Rt△AOB中，OB=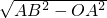
=8，
∴AC=12，BD=16，
∴S菱形ABCD=
AC•BD=×12×16=96．
故答案为：96．
点评：此题考查了菱形的性质以及勾股定理．此题难度不大，注意掌握数形结合思想的应用．
分析：由四边形ABCD是菱形，根据菱形的性质，可得AC⊥BD，AC=2OA，BD=2OB，又由勾股定理，即可求得OB的长，继而求得AC与BD的长，则可求得该菱形的面积．
解答：∵四边形ABCD是菱形，
∴AC⊥BD，AC=2OA，BD=2OB，
∵AB=10，AO=6，
在Rt△AOB中，OB=
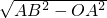=8，∴AC=12，BD=16，
∴S菱形ABCD=
AC•BD=×12×16=96．故答案为：96．
点评：此题考查了菱形的性质以及勾股定理．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
