题目内容
如图所示，在⊙O中，AB是弦，半径0C⊥AB，垂足为D，AB=8cm，CD=2cm，则0D等于（ ）分析：连接AO，由OC垂直于AB，利用垂径定理得到D为AB的中点，求出AD的长，设圆的半径为r，由OC-CD表示出OD，在直角三角形AOD中，利用勾股定理求出r的值，即可确定出OD的值．
解答：
解：连接AO，
∵OC⊥AB，∴D为AB的中点，
∴AD=4cm，
设圆的半径为r，
在Rt△AOD中，OD=OC-CD=（r-2）cm，
根据勾股定理得：OA2=AD2+OD2，即r2=16+（r-2）2，
解得：r=5，
则OD=5-2=3cm．
故选C
解：连接AO，∵OC⊥AB，∴D为AB的中点，
∴AD=4cm，
设圆的半径为r，
在Rt△AOD中，OD=OC-CD=（r-2）cm，
根据勾股定理得：OA2=AD2+OD2，即r2=16+（r-2）2，
解得：r=5，
则OD=5-2=3cm．
故选C
点评：此题考查了垂径定理，以及勾股定理，熟练掌握垂径定理是解本题的关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
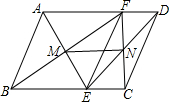如图所示，在?ABCD中，EF∥AB且交BC于点E，交AD于点F，连接AE，BF交于点M，连接CF，DE交于点N，求证：MN∥AD且MN=
如图所示，在△ABC中，∠C=90°，D是AC边上一点，且AD=DB=5，CD=3，求tan∠CBD和sinA．
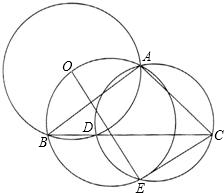如图所示，在△ABC中，已知D是BC边上的点，O为△ABD的外接圆圆心，△ACD的外接圆与△AOB的外接圆相交于A，E两点．求证：OE⊥EC．