题目内容
【题目】如图,在△ABC中,∠ACB=90°,AB=9,cosB= ![]() ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A,E之间的距离为 .
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A,E之间的距离为 . 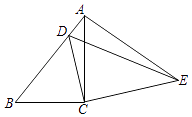
【答案】4 ![]()
【解析】解:∵在△ABC中,∠ACB=90°,AB=9,cosB= ![]() , ∴BC=ABcosB=9×
, ∴BC=ABcosB=9× ![]() =6,AC=
=6,AC= ![]() =3
=3 ![]() .
.
∵把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,
∴△ABC≌△EDC,BC=DC=6,AC=EC=3 ![]() ,∠BCD=∠ACE,
,∠BCD=∠ACE,
∴∠B=∠CAE.
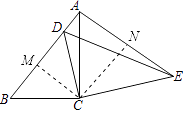
作CM⊥BD于M,作CN⊥AE于N,则∠BCM= ![]() ∠BCD,∠ACN=
∠BCD,∠ACN= ![]() ∠ACE,
∠ACE,
∴∠BCM=∠ACN.
∵在△ANC中,∠ANC=90°,AC=3 ![]() ,cos∠CAN=cosB=
,cos∠CAN=cosB= ![]() ,
,
∴AN=ACcos∠CAN=3 ![]() ×
× ![]() =2
=2 ![]() ,
,
∴AE=2AN=4 ![]() .
.
所以答案是4 ![]() .
.
【考点精析】关于本题考查的解直角三角形和旋转的性质,需要了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法);①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.

练习册系列答案
相关题目