Question

（2011山东烟台，24，10分）
已知：如图，在四边形ABCD中，∠ABC＝90°，CD⊥AD，AD²＋CD²＝2AB²．
（1）求证：AB＝BC；
（2）当BE⊥AD于E时，试证明：BE＝AE＋CD．

Answer 1

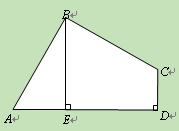
（1）证明：连接AC.
∵∠ABC＝90°，∴AB²＋BC²＝AC².
∵CD⊥AD，∴AD²＋CD²＝AC².
∵AD²＋CD²＝2AB²，∴AB²＋BC²＝2AB²，
∴AB＝BC.
（2）证明：过C作CF⊥BE于F.
∵BE⊥AD，∴四边形CDEF是矩形. ∴CD＝EF.
∵∠ABE＋∠BAE＝90°，∠ABE＋∠CBF＝90°，
∴∠BAE＝∠CBF，∴△BAE≌△CBF. ∴AE＝BF.
∴BE＝BF＋EF＝AE＋CD.解析:
略