题目内容
26、证明:不论m取何值时,关于x的方程(x-1)(x-2)=m2总有两个不相等的实数根.
分析:把方程变为一般式,计算出△,然后证明△>0即可.
解答:证明:方程化为一般式为:x2-3x+2-m2=0,
∴△=32-4(2-m2)=4m2+1,
∵不论m取何值,4m2≥0,
∴△>0.
所以不论m取何值时,关于x的方程(x-1)(x-2)=m2总有两个不相等的实数根.
∴△=32-4(2-m2)=4m2+1,
∵不论m取何值,4m2≥0,
∴△>0.
所以不论m取何值时,关于x的方程(x-1)(x-2)=m2总有两个不相等的实数根.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目

 ),若
),若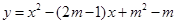 (
(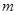 是常数,且
是常数,且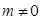 ).
).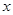 轴有两个交点;
轴有两个交点;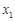 ,
,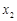 (其中
(其中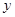 是关于
是关于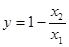 ,结合函数的图象回答:当自变量m的取值满足什么条件时,
,结合函数的图象回答:当自变量m的取值满足什么条件时,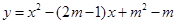 (
( 是常数,且
是常数,且 ).
). 轴有两个交点;
轴有两个交点; ,
, (其中
(其中 是关于
是关于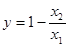 ,结合函数的图象回答:当自变量m的取值满足什么条件时,
,结合函数的图象回答:当自变量m的取值满足什么条件时,