题目内容
如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点 上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转180°,试解决下列问题:
上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转180°,试解决下列问题:
(1)画出四边形ABCD旋转后的图形;
(2)求点C旋转过程所经过的路径长;
(3)设点B旋转后的对应点为B′,求tan∠DAB′的值.
 解:(1)如图所示
解:(1)如图所示(2)易知点C的旋转路径是以O为圆心,OC为半径的半圆.
因为OC=
 =
= ,
,所以半圆的长为l=
 =
= .
. (3)B′D=
 =
= ,
,AB′=
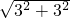 =3
=3 ,
,AD=
 =2
=2 ,
,所以AD2=B′D2+AB′2
所以△ADB′是直角三角形,且∠AB′D=90°.
所以tan∠DAB′=
 =
=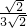 =
= .
. 分析:(1)连接BO、CO、并延长相同单位找到对应点,顺次连接即可.
(2)点C旋转过程所经过的路径是一段弧线,根据弧长公式即可计算.
(3)先利用网格计算出三角形的边长,得出三角形为直角三角形,再根据正切函数定义计算.
点评:本题综合考查了旋转变换作图和弧长公式的计算方法,及解直角三角形.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目


 (1)先化简,再求值:x(x-2)-(x+1)(x-1),其中x=10.
(1)先化简,再求值:x(x-2)-(x+1)(x-1),其中x=10.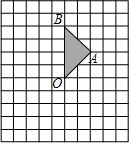 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABO的三个顶点A,B,O都在格点上.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABO的三个顶点A,B,O都在格点上.