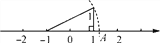
题目内容
已知:直线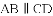
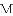
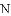
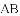
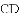
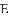
(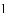
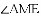
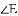
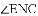
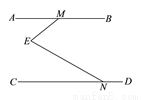
(
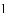
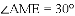
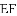
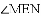
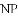
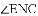
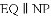
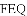

(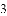
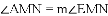
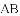
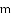
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
问题:探究函数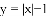
小华根据学习函数的经验,对函数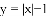
下面是小华的探究过程,请补充完整:
(
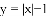
(
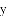
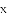
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
①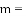
②若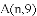
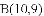
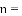
(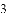
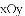
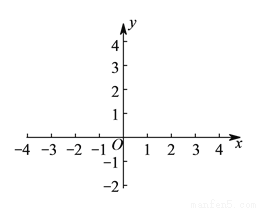
根据函数图象可得:
①该函数的最小值为__________.
②已知直线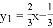 与函数
与函数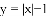
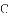
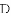
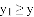 时
时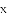
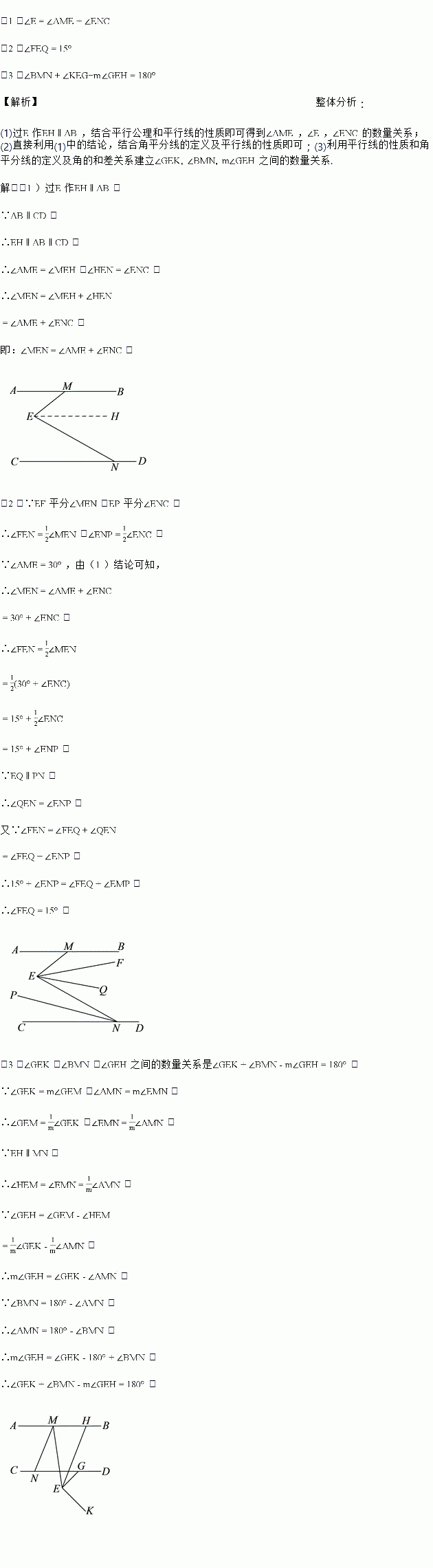


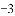
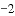
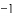
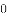
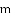
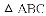
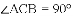
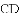
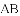
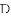
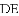
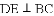
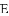
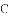
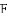
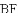
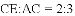
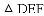
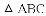

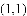
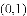
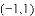
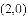
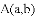
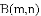
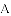
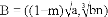 .若
.若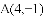
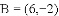
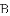
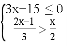 ,并将解集在数轴上表示出来.
,并将解集在数轴上表示出来.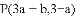
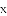
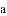
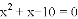 ,求代数式
,求代数式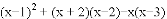 的值.
的值.