题目内容
两个反比例函数
，
在第一象限内的图像如图所示，点
，
，
，…，
在函数的图像上，它们的横坐标分别是
，
，
，…，
，纵坐标分别是1，3，5，…，共2013个连续奇数，过点，，，…，分别作y轴的平行线，与函数的图像交点依次是
（，
），
（，
），
（，
），…，
（，
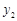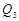），则
.
解析试题分析：因为点P1，P2，P3，…，P2010在反比例函数图象上，根据P1，P2，P3的纵坐标，推出P2010的纵坐标，再根据和的关系求解即可．
解：∵P1，P2，P3的纵坐标为1，3，5，是连续奇数
∴Pn的纵坐标为：2n-1
∴P2013的纵坐标为2×2013-1=4025
∵与在横坐标相同时，的纵坐标是的纵坐标的2倍
∴
．
考点：找规律-坐标的变化
点评：解题的关键是仔细分析所给图形的特征得到规律，再根据得到的规律解题即可.
练习册系列答案
巧学巧练系列答案
相关题目
(
)第一象限内的图像如图所示，△OP1B1，△B1P2B2均为等腰三角形，且OP1∥B1P2，其中点P1，P2在反比例函数
的值为 ．
位于第一象限的图象上，则k的值为 ．
的图象经过点（﹣2，3），则k的值为 ．
的图象经过点（1，2），则k= 。
、
分别与双曲线
相交于A、B、P、Q四点，其中A、P两点在第一象限，设A点坐标为（3，1）．
值及
点坐标；（4分）
，求P点坐标．（4分）
与反比例函数
的图象相交于点A（－1，a），并且与x轴相交于点B．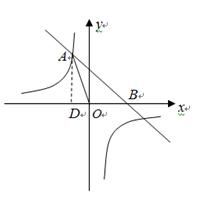
和
在第一象限内的图象分别是C1和C2，设点P在C1上，PA⊥x轴于点A，交C2于点B，则△POB的面积为 ．