题目内容
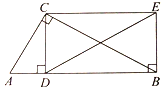
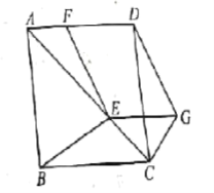
【题目】如图，在正方形
中，对角线
上有一点
，连结
，作
交
于点
．过点作直线
的对称点
，连接
求证：
求证：四边形
为平行四边形；
若
有可能成为菱形吗?如果可能，求此时
长；如果不可能，请说明理由．
【答案】（1）详见解析；（2）详见解析；（3）
【解析】
（1）利用对称的性质得出
，
，再根据正方形的性质得出
，
，从而可证明结论；
（2）根据点
与点
关于直线
对称，推出
，再根据正方形的性质得出
，从而推出
，再利用（1）中结论
，得出
，可得出
，推出
，继而证明结论；
（3）过点作
于点
于点
，根据已知条件结合示意图可证明
，得到
，又因为
，继而得出
，当四边形
为菱形时，
为等边三角形，从而得出
，设
， 则
，
，再结合AB=4求x的值，进一步计算即可得出答案．
解：
证明：
点与点关于直线对称，
，，
四边形
为正方形，
，
；
点与点关于直线对称，
，
，
，
，
∴∠GEC＝∠BCE＝∠CGE＝45°，
，
，
由得，
，
，
，
四边形为平行四边形；
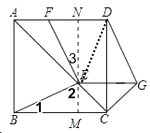
如图所示，过点作于点于点，连接DE，
，
，
，
，
，
，
，
四边形为正方形，
关于
对称，
，
，
当四边形为菱形时，
，
为等边三角形，
，
设，则，
，
，
四边形为正方形，
，
，
，
.
练习册系列答案
相关题目
