题目内容
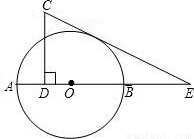
（2002•扬州）已知：如图，AB是⊙O的直径，CD⊥AB，垂足为D，CE切⊙O于点F，交AB的延长线于点E，求证：EF•EC=EO•ED．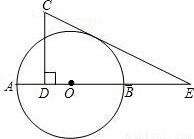
【答案】分析：先把等积式变为比例式得
，即只要证出△EFO∽△EDC，根据相似三角形的对应边成比例即可得到结论．
解答：
证明：连接OF，则由题可知∠OFE=90°，
又∵CD⊥AB，
∴∠CDE=∠OFE=90°．
又∠FEO=∠DEC，
∴△EFO∽△EDC．
∴
．
即EF•EC=EO•ED．
点评：此题主要是考查了三角形相似的判定的理解及运用．
，即只要证出△EFO∽△EDC，根据相似三角形的对应边成比例即可得到结论．解答：
证明：连接OF，则由题可知∠OFE=90°，又∵CD⊥AB，
∴∠CDE=∠OFE=90°．
又∠FEO=∠DEC，
∴△EFO∽△EDC．
∴
．即EF•EC=EO•ED．
点评：此题主要是考查了三角形相似的判定的理解及运用．
练习册系列答案
相关题目
