题目内容
3.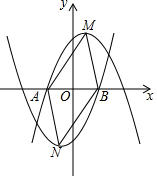 如图,在平面直角坐标系中,抛物线y=-(x-h)2+2(h>0)的顶点为M,与x轴负半轴的交点为A,抛物线y=(x+h)2-2的顶点为N,与x轴正半轴的交点为B,若AB=2h,则四边形MANB的面积为2$\sqrt{2}$.
如图,在平面直角坐标系中,抛物线y=-(x-h)2+2(h>0)的顶点为M,与x轴负半轴的交点为A,抛物线y=(x+h)2-2的顶点为N,与x轴正半轴的交点为B,若AB=2h,则四边形MANB的面积为2$\sqrt{2}$.
分析 先根据抛物线的解析式分别求A、B两点的坐标,表示AB的长,根据AB=2h,列式可得4h=2$\sqrt{2}$,最后利用面积和可求得结论.
解答 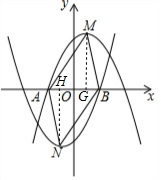 解:y=-(x-h)2+2,
解:y=-(x-h)2+2,
当y=0时,-(x-h)2+2=0,
(x-h)2=2,
x-h=$±\sqrt{2}$,
${x}_{1}=h-\sqrt{2}$,${x}_{2}=h+\sqrt{2}$,
∵A为抛物线与x轴负半轴的交点,
∴A(h-$\sqrt{2}$,0),
∴OA=$\sqrt{2}$-h,
y=(x+h)2-2,
当y=0时,(x+h)2-2=0,
(x+h)2=2,
x+h=$±\sqrt{2}$,
x1=-h-$\sqrt{2}$,x2=-h+$\sqrt{2}$,
∵B为抛物线与x轴正半轴的交点,
∴B(-h+$\sqrt{2}$,0),
∴OB=-h+$\sqrt{2}$,
∴AB=OA+OB=2h,
∴2h=$\sqrt{2}$-h+$\sqrt{2}$-h,
4h=2$\sqrt{2}$,
过M作MG⊥x轴于G,过N作NH⊥x轴于H,
由题意得:M(h,2),N(-h,-2),
∴MG=NH=2,
∵S四边形MANB=S△MAB+S△NAB=$\frac{1}{2}$AB•MG+$\frac{1}{2}$AB•NH=$\frac{1}{2}$AB•(MG+NH)=$\frac{1}{2}$•2h•(2+2)=4h=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题考查了抛物线与x轴的交点、一元二次方程的解、四边形和三角形的面积,利用图形与坐标特点表示AB的长,列等式是关键.

练习册系列答案
相关题目
13.在“阳光体育节”活动中,某校对六(1)班、(2)班同学各50人参加体育活动的情况进行了调查,结果如图所示.下列说法中( )是正确的.
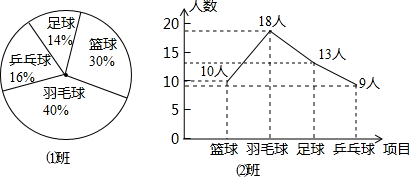

| A. | 喜欢乒乓球的人数(1)班比(2)班多 | B. | 喜欢足球的人数(1)班比(2)班多 | ||
| C. | 喜欢羽毛球的人数(1)班比(2)班多 | D. | 喜欢篮球的人数(2)班比(1)班多 |
14.计算5a-a结果正确的是( )
| A. | 4a | B. | 5 | C. | -4 | D. | -4a |
13. 如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )
 如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )| A. | 2$\sqrt{3}$ | B. | $\frac{π}{6}$ | C. | 4$\sqrt{3}$-$\frac{2π}{3}$ | D. | 2$\sqrt{3}$-$\frac{2π}{3}$ |
 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,动点D从点A出发,沿线段AC以每秒1个单位的速度向终点C运动,动点E同时从点B出发,以每秒2个单位的速度沿射线BC方向运动,当点D停止时,点E也随之停止,连结DE,当C、D、E三点不在同一直线上时,以ED、EC我邻边作?ECFD,设点D运动的时间为t(秒).
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,动点D从点A出发,沿线段AC以每秒1个单位的速度向终点C运动,动点E同时从点B出发,以每秒2个单位的速度沿射线BC方向运动,当点D停止时,点E也随之停止,连结DE,当C、D、E三点不在同一直线上时,以ED、EC我邻边作?ECFD,设点D运动的时间为t(秒).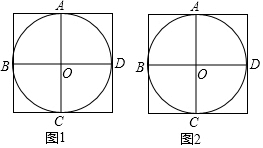 在图1、图2中,⊙O经过了正方形网格中的格点A、B、C、D,现请你仅用无刻度的直尺分别在图1、图2中画出一个满足下列条件的∠P.
在图1、图2中,⊙O经过了正方形网格中的格点A、B、C、D,现请你仅用无刻度的直尺分别在图1、图2中画出一个满足下列条件的∠P.