题目内容
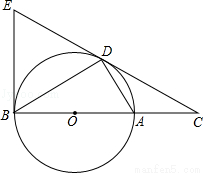
(2013年四川泸州2分)如图,在等腰直角△ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:
(1)图形中全等的三角形只有两对;(2)△ABC的面积等于四边形CDOE的面积的2倍;(3)CD+CE=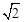 OA;(4)AD2+BE2=2OP•OC.其中正确的结论有【 】
OA;(4)AD2+BE2=2OP•OC.其中正确的结论有【 】

A.1个 B.2个 C.3个 D.4个
C。
【解析】结论(1)错误。理由如下:
图中全等的三角形有3对,分别为△AOC≌△BOC,△AOD≌△COE,△COD≌△BOE:
由等腰直角三角形的性质,可知OA=OC=OB,易得△AOC≌△BOC。
∵OC⊥AB,OD⊥OE,∴∠AOD=∠COE。
在△AOD与△COE中,∵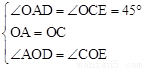 ,∴△AOD≌△COE(ASA)。
,∴△AOD≌△COE(ASA)。
同理可证:△COD≌△BOE。
结论(2)正确。理由如下:
∵△AOD≌△COE,∴S△AOD=S△COE。
∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC=S△ABC,
即△ABC的面积等于四边形CDOE的面积的2倍。
结论(3)正确。理由如下:
∵△AOD≌△COE,∴CE=AD。∴CD+CE=CD+AD=AC=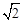 OA。
OA。
结论(4)正确。理由如下:
∵△AOD≌△COE,∴AD=CE。
∵△COD≌△BOE,∴BE=CD。
在Rt△CDE中,由勾股定理得:CD2+CE2=DE2,∴AD2+BE2=DE2。
∵△AOD≌△COE,∴OD=OE。
又∵OD⊥OE,∴△DOE为等腰直角三角形。∴DE2=2OE2,∠DEO=45°。
∵∠DEO=∠COE=45°,∠COE=∠COE,∴△OEP∽△OCE。∴ ,即OP•OC=OE2。
,即OP•OC=OE2。
∴DE2=2OE2=2OP•OC。∴AD2+BE2=2OP•OC。
综上所述,正确的结论有3个。故选C。
考点:等腰直角三角形的性质,全等三角形的判定和性质,勾股定理,相似三角形的判定和性质。

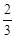 ,求BE的长.
,求BE的长.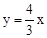 与反比例函数
与反比例函数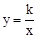 (x>0)的图象交于点A.将
(x>0)的图象交于点A.将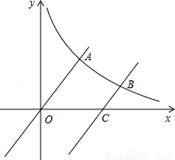
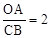 ,求反比例函数的解析式.
,求反比例函数的解析式.