题目内容
已知抛物线y=-x2+mx-m+2.
(Ⅰ)若抛物线与x轴的两个交点A、B分别在原点的两侧,并且AB=![]() ,试求m的值;
,试求m的值;
(Ⅱ)设C为抛物线与y轴的交点,若抛物线上存在关于原点对称的两点M、N,并且 △MNC的面积等于27,试求m的值
(Ⅰ)1
(Ⅱ)-7
解析:解: (I)设点A(x1,0),B(x2,0).
则x1 ,x2是方程 x2-mx+m-2=0的两根.
∵x1 + x2 =m , x1·x2 =m-2 <0 即m<2;
又AB=∣x1- x2∣=![]() ,∴m2-4m+3=0 .
,∴m2-4m+3=0 .
 解得:m=1或m=3(舍去) ,
解得:m=1或m=3(舍去) ,
∴m的值为1.
(II)设M(a,b),则N(-a,-b).
∵M、N是抛物线上的两点,
∴
①+②得:-2a2-2m+4=0.
∴a2=-m+2.
∴当m<2时,才存在满足条件中的两点M、N.
∴![]() .
.
这时M、N到y轴的距离均为![]() ,
,
又点C坐标为(0,2-m),而S△M N C = 27 ,
∴2×![]() ×(2-m)×
×(2-m)×![]() =27.
=27.
∴解得m=-7

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
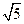 ,试求m的值;
,试求m的值; 直角坐标系中,用列表描点法作出抛物线的图象,并根据图象写出x取何值时,函
直角坐标系中,用列表描点法作出抛物线的图象,并根据图象写出x取何值时,函