题目内容
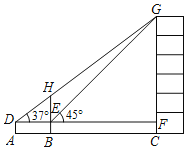
【题目】如图,在平行四边形![]() 中,
中,![]() ,垂足为点
,垂足为点![]() ,将平行四边形
,将平行四边形![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 的位置,点
的位置,点![]() 落在点
落在点![]() 的位置,折痕为
的位置,折痕为![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的度数;
的度数;
(3)连接![]() ,求证:四边形
,求证:四边形![]() 是矩形.
是矩形.
【答案】(1)见解析(2)60°(3)见解析
【解析】
(1)根据折叠的性质,得到∠A=∠G,AD=DG,再根据轴对称的性质即可得到AE=FG,进而运用SAS判定△ADE≌△GDF;
(2)根据BD=![]() AB,可得sinA=
AB,可得sinA=![]() ,进而得到∠A=30°,再根据DF=CF=FG,即可得到∠FDG=∠DGF=∠A=30°,即可得出∠CFG=∠FDG+∠DGF=60°;
,进而得到∠A=30°,再根据DF=CF=FG,即可得到∠FDG=∠DGF=∠A=30°,即可得出∠CFG=∠FDG+∠DGF=60°;
(3)连接CG,根据BC=DG,BC∥DG,可得四边形BCGD是平行四边形,再根据∠CBD=90°,即可得到四边形BCGD是矩形.
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,∠A=∠C,
由折叠可知,BC=DG,CF=FG,∠G=∠C,EF垂直平分BD,
∴∠A=∠G,AD=DG,
又∵AD⊥BD,
∴EF∥AD∥BC,
∴点E、F分别平分AB、CD,
∴AE=BE=![]() AB=
AB=![]() CD=CF=DF,
CD=CF=DF,
∴AE=FG,
∴△ADE≌△GDF;
(2)∵AE=BD,AE=BE=![]() AB,
AB,
∴BD=![]() AB,
AB,
∴sinA=![]() ,
,
∴∠A=30°,
∵DF=CF=FG,
∴∠FDG=∠DGF=∠A=30°,
∴∠CFG=∠FDG+∠DGF=60°;
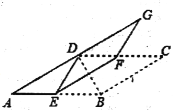
(3)如图,连接CG.

由折叠可知,BC=DG,BC∥DG,
∴四边形BCGD是平行四边形,
∵AD⊥BD,AD∥BC,
∴BC⊥BD,
∴∠CBD=90°,
∴四边形BCGD是矩形.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案【题目】如图所示,有一个可以自由转动的转盘,其盘面分为4等份,在每一等份分别标有对应的数字2,3,4,5.小明打算自由转动转盘10次,现已经转动了8次,每一次停止后,小明将指针所指数字记录如下:
次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 |
数字 | 3 | 5 | 2 | 3 | 3 | 4 | 3 | 5 |
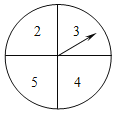
(1)求前8次的指针所指数字的平均数.
(2)小明继续自由转动转盘2次,判断是否可能发生“这10次的指针所指数字的平均数不小于3.3,且不大于3.5”的结果?若有可能,计算发生此结果的概率,并写出计算过程;若不可能,说明理由.(指针指向盘面等分线时为无效转次.)
【题目】为了解学生的课外阅读情况,七(1)班针对“你最喜爱的课外阅读书目”进行调查(每名学生必须选一类且只能选一类阅读书目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选类别人数统计表
类别 | 男生(人) | 女生(人) |
文学类 | 12 | 8 |
史学类 |
| 5 |
科学类 | 6 | 5 |
哲学类 | 2 |
|

根据以上信息解决下列问题
(1)![]() ,
,![]() ;
;
(2)扇形统计图中“科学类”所对应扇形圆心角度数为 ![]() ;
;
(3)从选哲学类的学生中,随机选取两名学生参加学校团委组织的辩论赛,请用树状图或列表法求出所选取的两名学生都是男生的概率.
【题目】甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.
施工时间/天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
累计完成施工量/米 | 35 | 70 | 105 | 140 | 160 | 215 | 270 | 325 | 380 |
下列说法错误的是( )
A. 甲队每天修路20米
B. 乙队第一天修路15米
C. 乙队技术改进后每天修路35米
D. 前七天甲,乙两队修路长度相等