题目内容
如图6,用水平线与竖直线将平面分成若干个边长为1的正方形格子,点O、A、B均在正方形格子的顶点(格点)处,其中点O与点A位于同一水平线上,相距a格,点O与点B位于同一竖直线上,相距b格.
(1)若a=5,b=4,则△OAB中(包括三条边)共有多少个格点?
(2)若a,b互质,则在线段AB上(不包括A、B两点)是否有格点?证明你的结论.
(3)若a,b互质,且a>b>8,△OAB中(包括三条边)共有67个格点,求a,b的值.
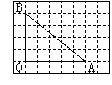
(1)如图2,a=5,b=4,△OAB中(包括三条边)的格点的个数为1+2+3+4+6=16.
(2)若a,b互质,假设线段AB上存在某一点P(恰为格点),可设点P到点O的水平距离为x,竖直距离为y(x,y均为整数),则
S△AOB= S△AOP+S△BOP=![]() ay+
ay+![]() bx,
bx,
所以![]() ab=
ab=![]() ay+
ay+![]() bx,
bx,
即ab=ay+bx,ay=b(a-x).
因为a,b互质,
所以a-x是a的倍数,它与a-x<a矛盾,
因此,假设不正确,即线段AB上(除A、B两点外)不存在其它格点.
(3)由(2)知,线段AB上(除A、B两点外)不存在其它的格点.
以OA、OB为边作一个矩形OACB,则在△CAB中格点的个数与△OAB中格点的个数相同,且只有A、B两点是公共的,而矩形OACB中格点的个数为(a+1)(b+1).
因此,(a+1)(b+1)+2=2×67=134,
(a+1)(b+1)=132=2×2×3×11.
由a>b>8,得a+1=12,b+1=11,
即a=11,b=10.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
一般地,由n条不在同一直线上的线段首尾顺次连接组成的平面图形称为n边形,又称为多边形.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x.
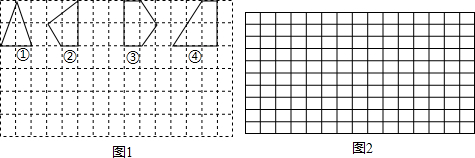
(1)如图1中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请把表格补充完整,并写出S与x之间的关系式.
答:S=______.
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | … |
注:备用表格供你探索使用(作图时,请使用铅笔).

 第
第