题目内容
(1)阅读下列材料,补全证明过程:
已知:如图,矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G.求证:点G是线段BC的一个三等分点.

证明:在矩形ABCD中,OE⊥BC,DC⊥BC,
∴OE∥DC,∵ ,∴
,∴ =
= =
= ∴
∴ =
= .…
.…
(2)请你仿照(1)的画法,在原图上画出BC的一个四等分点(要求保留画图痕迹,可不写画法及证明过程).

解:(1)在矩形ABCD中,OB=OC,OE⊥BC于E,
∴E为BC的中点,
又O为BD的中点,
∴OE为△BCD的中位线,
∴ .
.
∵OE⊥BC,DC⊥BC,
∴OE∥DC,
∴△OEF∽△CDF.
∴ =
= =
= ,
,
∴ =
= ,
, .
.
又∵FG∥DC,
 =
= ,
,
∴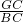 =
= =
=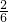 =
= .
.
∴点G是BC的一个三等分点;
(2)依题意画图如下:如图,点I即为所求.

分析:(1)欲证点G是线段BC的一个三等分点,由图可知,只需证明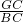 =
= 即可.由于矩形ABCD中,OB=OC,OE⊥BC于E,则E为BC的中点.易证OE为△BCD的中位线,则
即可.由于矩形ABCD中,OB=OC,OE⊥BC于E,则E为BC的中点.易证OE为△BCD的中位线,则 .由OE∥CD,得出
.由OE∥CD,得出 =
= =
= ,由比例的性质可知,
,由比例的性质可知, .再由FG∥DC,得出
.再由FG∥DC,得出 =
= ,而BC=2EC,从而求出
,而BC=2EC,从而求出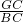 =
= ;
;
(2)由(1)的画法,可知连接DG交OC于点H,作HI⊥BC于I,则点I是线段BC的一个四等分点.
点评:本题考查平行线分线段成比例定理,要根据平行找准对应关系.
∴E为BC的中点,
又O为BD的中点,
∴OE为△BCD的中位线,
∴
 .
.∵OE⊥BC,DC⊥BC,
∴OE∥DC,
∴△OEF∽△CDF.
∴
 =
= =
= ,
,∴
 =
= ,
, .
.又∵FG∥DC,
 =
= ,
,∴
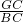 =
= =
=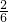 =
= .
.∴点G是BC的一个三等分点;
(2)依题意画图如下:如图,点I即为所求.

分析:(1)欲证点G是线段BC的一个三等分点,由图可知,只需证明
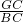 =
= 即可.由于矩形ABCD中,OB=OC,OE⊥BC于E,则E为BC的中点.易证OE为△BCD的中位线,则
即可.由于矩形ABCD中,OB=OC,OE⊥BC于E,则E为BC的中点.易证OE为△BCD的中位线,则 .由OE∥CD,得出
.由OE∥CD,得出 =
= =
= ,由比例的性质可知,
,由比例的性质可知, .再由FG∥DC,得出
.再由FG∥DC,得出 =
= ,而BC=2EC,从而求出
,而BC=2EC,从而求出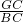 =
= ;
;(2)由(1)的画法,可知连接DG交OC于点H,作HI⊥BC于I,则点I是线段BC的一个四等分点.
点评:本题考查平行线分线段成比例定理,要根据平行找准对应关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目