题目内容
如图，点P是线段AB的黄金分割点，且AP＞BP，设以AP为边长的正方形面积为S1，以PB为宽和以AB为长的矩形面积为S2，试比较S1与S2的大小．
解：∵点P是线段AB的黄金分割点，且AP＞BP，
∴AP2=BP×AB，
又∵S1=AP2，S2=PB×AB，
∴S1=S2．
分析：根据黄金分割的定义可得AP2=BP×AB，得出S1，S2的表达式即可比较S1与S2的大小．
点评：本题考查了黄金分割的知识，关键是得出AP2=BP×AB，属于基础题．
∴AP2=BP×AB，
又∵S1=AP2，S2=PB×AB，
∴S1=S2．
分析：根据黄金分割的定义可得AP2=BP×AB，得出S1，S2的表达式即可比较S1与S2的大小．
点评：本题考查了黄金分割的知识，关键是得出AP2=BP×AB，属于基础题．
练习册系列答案
相关题目
如图，点C是线段AB的中点，点D是线段BC的中点，下面等式不正确的是（ ）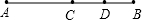
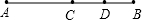
| A、CD=AD-BC | ||
| B、CD=AC-DB | ||
C、CD=
| ||
D、CD=
|
10、如图，点D是线段AB与线段BC的垂直平分线的交点，∠B=40°，则∠ADC等于（ ）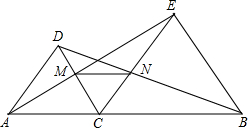
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE，AE与CD相交于点M，BD和CE相交于点N．
如图，点C是线段AB的中点，点D是线段CB上任意一点，则下列表示线段关系的式子不正确的是（ ）
如图，点C是线段AB的中点，点D是线段BC的中点，则下列结论中错误的是（ ）