题目内容
【题目】如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为() 
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
【答案】C
【解析】解:如图,过D作DF⊥AF于F, ∵点B的坐标为(1,3),
∴AO=1,AB=3,
根据折叠可知:CD=OA,
而∠D=∠AOE=90°,∠DEC=∠AEO,
∴△CDE≌△AOE,
∴OE=DE,OA=CD=1,
设OE=x,那么CE=3﹣x,DE=x,
∴在Rt△DCE中,CE2=DE2+CD2 ,
∴(3﹣x)2=x2+12 ,
∴x= ![]() .
.
又DF⊥AF,
∴DF∥EO,
∴△AEO∽△ADF,
而AD=AB=3,
∴AE=CE=3﹣ ![]() =
= ![]() ,
,
∴ ![]() ,
,
即 ![]() ,
,
∴DF= ![]() ,AF=
,AF= ![]() .
.
∴OF= ![]() ﹣1=
﹣1= ![]() .
.
∴点D的坐标为(﹣ ![]() ,
, ![]() ).
).
故选:C.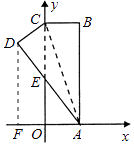
【考点精析】通过灵活运用矩形的性质和坐标与图形变化-对称,掌握矩形的四个角都是直角,矩形的对角线相等;关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y);关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)即可以解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目