Question

【题目】综合题

如图1，为直线上一点，过点作射线，，将一直角三角板（）的直角顶点放在点处，一边在射线上，另一边与都在直线的上方．

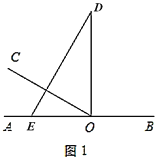
（1）将图1中的三角板绕点以每秒的速度沿顺时针方向旋转一周，如图2，经过秒后，恰好平分．

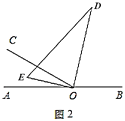
①此时的值为______；（直接填空）

②此时是否平分？请说明理由．

（2）在（1）问的基础上，若三角板在转动的同时，射线也绕点以每秒的速度沿顺时针方向旋转一周，如图3，那么经过多长时间平分？请说明理由；

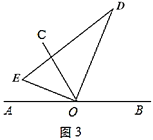
（3）在（2）问的基础上，经过多长时间平分？

Answer 1

【答案】（1）①3；②是，理由见解析；（2）经过5秒或69秒时，平分；（3）经过秒时，平分．

【解析】

（1）①先求出时的的度数，再求出当恰好平分时，最后根据旋转的角度等于前后两次所求度数的差列出方程即得．

②在①中求出的的条件下，求出此时的的度数即可．

（2）先根据平分可将旋转度数与三角板旋转度数之差分为、和三种情况， 然后以平分为等量关系列出方程即得．

（3）先根据旋转速度与三角板旋转速度判断平分应该在两者旋转过之后，然后用分别表示出与的度数，最后依据平分为等量关系列出方程即可．

（1）①当时

∵，

∴

当直角三角板绕点旋转秒后

∴

∵，

∴

∵恰好平分

∴

∴

∴．

②是，理由如下：

∵转动3秒，∴，

∴，

∴，即平分．

（2）直角三角板绕点旋转一周所需的时间为（秒），射线绕点旋转一周所需的时间为

（秒），

设经过秒时，平分，

由题意：①，

解得：，

②，

解得：，不合题意，

③∵射线绕点旋转一周所需的时间为（秒），45秒后停止运动，

∴旋转时，平分，

∴（秒），

综上所述，秒或69秒时，平分．

（3）由题意可知，旋转到与重合时，需要（秒），

旋转到与重合时，需要（秒），

所以比早与重合，

设经过秒时，平分．

由题意：，

解得：，

所以经过秒时，平分．