题目内容
如图是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为_米.(结果精确到0.1米,参考数据:  ≈1.41,
≈1.41,  ≈1.73)
≈1.73)

【答案】2.9
【解析】试题分析:在Rt△AMD中,∠MAD=45°,AM=4米,可得MD=4米;在Rt△BMC中,BM=AM+AB=12米,∠MBC=30°,可求得MC=4 米,所以警示牌的高CD=4
米,所以警示牌的高CD=4 -4=2.9米.
-4=2.9米.
考点:解直角三角形.
【题型】填空题
【结束】
16
如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=_____.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目


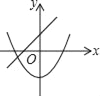 B.
B. 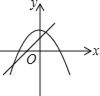 C.
C. 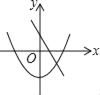 D.
D. 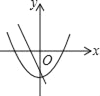
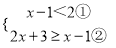 ,请结合题意填空,完成本题的解答.
,请结合题意填空,完成本题的解答.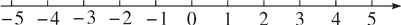
 B.
B. C.
C. D.
D.
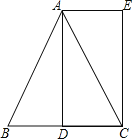
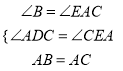
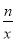 (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.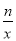 的解集.
的解集.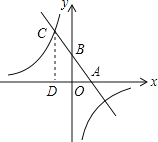

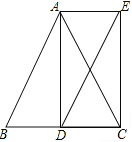
 B. AD,AE将∠BAC三等分
B. AD,AE将∠BAC三等分 ,又∵∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC﹣∠BAD=72°,∴∠ADC=∠DAC,∴CD=CA=BA,∴BD=BC﹣CD=BC﹣AB,则
,又∵∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC﹣∠BAD=72°,∴∠ADC=∠DAC,∴CD=CA=BA,∴BD=BC﹣CD=BC﹣AB,则 =
= ,即
,即 S△ABD,S△CEG=
S△ABD,S△CEG= x+1与y轴交于点A,与x轴交于点D,抛物线y=
x+1与y轴交于点A,与x轴交于点D,抛物线y= 
