题目内容
 如图,E,F,G,H分别是正方形ABCD各边的中点,要使中间阴影部分小正方形的面积是5,那么大正方形的边长应该是
如图,E,F,G,H分别是正方形ABCD各边的中点,要使中间阴影部分小正方形的面积是5,那么大正方形的边长应该是
- A.

- B.
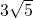
- C.5
- D.

C
分析:设正方形的边长为2X,则AB=2X,BF=X,根据正方形的性质得△BFW∽△AFB,从而可求得WF,BW,AS,从而可求得SW的长,则根据面积公式不难求得大正方形的边长.
解答: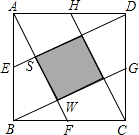 解:设正方形的边长为2X,则AB=2X,BF=X,
解:设正方形的边长为2X,则AB=2X,BF=X,
由勾股定理得,AF= X,由同角的余角相等,易得△BFW∽△AFB,
X,由同角的余角相等,易得△BFW∽△AFB,
∴BF:AF=BW:AB=WF:BF,得,WF= X,BW=
X,BW= X,同理,AS=
X,同理,AS= X,
X,
∴SW=AF-AS-WF= X
X
∵阴影部分小正方形的面积是5
∴( X)2=5,得X=
X)2=5,得X=
∴AB=5.
故选C.
点评:本题利用了正方形的性质,相似三角形的判定和性质,勾股定理求解.
分析:设正方形的边长为2X,则AB=2X,BF=X,根据正方形的性质得△BFW∽△AFB,从而可求得WF,BW,AS,从而可求得SW的长,则根据面积公式不难求得大正方形的边长.
解答:
 解:设正方形的边长为2X,则AB=2X,BF=X,
解:设正方形的边长为2X,则AB=2X,BF=X,由勾股定理得,AF=
 X,由同角的余角相等,易得△BFW∽△AFB,
X,由同角的余角相等,易得△BFW∽△AFB,∴BF:AF=BW:AB=WF:BF,得,WF=
 X,BW=
X,BW= X,同理,AS=
X,同理,AS= X,
X,∴SW=AF-AS-WF=
 X
X∵阴影部分小正方形的面积是5
∴(
 X)2=5,得X=
X)2=5,得X=
∴AB=5.
故选C.
点评:本题利用了正方形的性质,相似三角形的判定和性质,勾股定理求解.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.