题目内容
 如图,在一个3×5的正方形网格中,△ABC的顶点A,B,C在单位正方形顶点上,请你在图中画一个△A1B1C1,使得△A1B1C1∽△ABC,且点A1,B1,C1都在单位正方形的顶点上.
如图,在一个3×5的正方形网格中,△ABC的顶点A,B,C在单位正方形顶点上,请你在图中画一个△A1B1C1,使得△A1B1C1∽△ABC,且点A1,B1,C1都在单位正方形的顶点上.分析:首先得出∠ABC=135°,进而利用相似三角形的判定与性质得出可以把这对应边比值看作
:2,2:2
等,进而得出答案.
| 2 |
| 2 |
解答: 解:由图可知∠ABC=135°,不妨设单位正方形的边长为1个单位,则AB:BC=1:
解:由图可知∠ABC=135°,不妨设单位正方形的边长为1个单位,则AB:BC=1:
,
由此推断,所画三角形必有一角为135°,且夹该角的两边之比为1:
,
也可以把这一比值看作
:2,2:2
等,以此为突破口,在图连出
和2,2和2
等线段,
即得△EDF∽△GDH∽△FMN∽△ABC,
如图所示.即图中的△EDF、△GDH、△FMN均可视为△A1B1C1.
 解:由图可知∠ABC=135°,不妨设单位正方形的边长为1个单位,则AB:BC=1:
解:由图可知∠ABC=135°,不妨设单位正方形的边长为1个单位,则AB:BC=1:| 2 |
由此推断,所画三角形必有一角为135°,且夹该角的两边之比为1:
| 2 |
也可以把这一比值看作
| 2 |
| 2 |
| 2 |
| 2 |
即得△EDF∽△GDH∽△FMN∽△ABC,
如图所示.即图中的△EDF、△GDH、△FMN均可视为△A1B1C1.
点评:此题主要考查了相似三角形的判定与性质,得出三角形边长之间的关系是解题关键.

练习册系列答案
相关题目
 25、如图,在一个10×10的正方形DEFG网格中有一个△ABC.
25、如图,在一个10×10的正方形DEFG网格中有一个△ABC. 20、如图,在一个“羊”字的图形中有16个圆圈,请你仿照九宫图的玩法,将圆圈中填上从1至16共16个连续数字;使两个羊角、羊脸,两个羊腮,各个加起来的总和都一样.
20、如图,在一个“羊”字的图形中有16个圆圈,请你仿照九宫图的玩法,将圆圈中填上从1至16共16个连续数字;使两个羊角、羊脸,两个羊腮,各个加起来的总和都一样. 如图,在一个含30°的三角板ABC中,将三角板沿着AB所在直线翻转180°得到△ABF,再将三角板绕点C顺时针方向旋转60°得到△DEC,点F在AC上,连接AE.
如图,在一个含30°的三角板ABC中,将三角板沿着AB所在直线翻转180°得到△ABF,再将三角板绕点C顺时针方向旋转60°得到△DEC,点F在AC上,连接AE.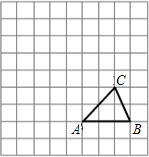 (2012•黑河)顶点在网格交点的多边形叫做格点多边形,如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.
(2012•黑河)顶点在网格交点的多边形叫做格点多边形,如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度. 如图,在一个4×4的正方形网格中,若两个阴影部分的三角形绕某点旋转一定的角度后能互相重合,则其旋转中心可能是图中的( )
如图,在一个4×4的正方形网格中,若两个阴影部分的三角形绕某点旋转一定的角度后能互相重合,则其旋转中心可能是图中的( )