题目内容
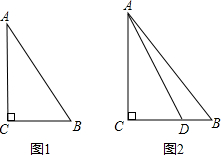
我国是发现和研究勾股定理最古老的国家之一，勾股定理如下：在直角三角形中，两直角边的平方和等于斜边的平方，如图1，△ABC是直角三角形，∠C是直角，则有AC2+BC2=AB2，请解答下列问题：
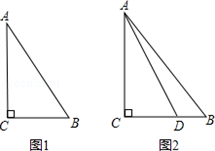
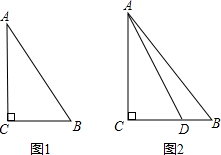
（1）如图2，△ABC是直角三角形，∠C是直角，直角边AC=4，斜边AB=5，请用勾股定理计算直角边CB，则CB=_______；
（2）如图2，在（1）的条件下，D是BC边上一点且2CD﹣3BD=1，则CD= _________ ，BD=__________；
（3）如图2，在（2）的条件下，若∠DAB=α，用课堂学习过的知识求∠B（用α表示）。
（1）如图2，△ABC是直角三角形，∠C是直角，直角边AC=4，斜边AB=5，请用勾股定理计算直角边CB，则CB=_______；
（2）如图2，在（1）的条件下，D是BC边上一点且2CD﹣3BD=1，则CD= _________ ，BD=__________；
（3）如图2，在（2）的条件下，若∠DAB=α，用课堂学习过的知识求∠B（用α表示）。
解：（1）由题意得，CB2=AB2-AC2，
∴可求得CB=
=3；
（2）由已知条件可得：
，
解得：
；
（3）tan∠ADC=
=2，
∴∠ADC=arctan2，
故可得∠B=∠ADC-∠DAB=arctan2-α。
∴可求得CB=
=3；（2）由已知条件可得：
，解得：
；（3）tan∠ADC=
=2，∴∠ADC=arctan2，
故可得∠B=∠ADC-∠DAB=arctan2-α。
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
（m2-1）和c=
