题目内容
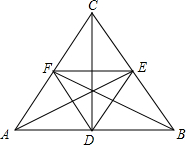如图，D，E，F为等边三角形ABC三边中点，AE、BF、CD交于O，DE，EF，FD为三条中位线，则图中能数出不同的直角三角形的个数是（ ）分析：根据等边三角形的“三线合一”的性质来找直角三角形．
解答：解：①∵DE，EF，FD为等边△ABC三条中位线，
∴AB=AC=BC，
∴EF
AB，ED
AC，
∴四边形CEDF是菱形，
∴EF⊥CD，
∴在菱形CEDF中有6个不同的直角三角形：Rt△CEG、Rt△CFG、Rt△DGE、Rt△DFG、Rt△EOG、Rt△FOG；
同理，在菱形ADEF、菱形BEFD中各有6个不同的直角三角形；
②∵D为等边三角形ABC三边中点，
∴CD⊥AB，
∴△ADC、△BDC、AOD、△BOD是直角三角形；
同理，以BF、AE为直角边的三角形各有4个；
综上所述，图中能数出的直角三角形由6×3+4×3=30（个）；
故选C．
∴AB=AC=BC，
∴EF
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
∴四边形CEDF是菱形，
∴EF⊥CD，
∴在菱形CEDF中有6个不同的直角三角形：Rt△CEG、Rt△CFG、Rt△DGE、Rt△DFG、Rt△EOG、Rt△FOG；
同理，在菱形ADEF、菱形BEFD中各有6个不同的直角三角形；
②∵D为等边三角形ABC三边中点，
∴CD⊥AB，
∴△ADC、△BDC、AOD、△BOD是直角三角形；
同理，以BF、AE为直角边的三角形各有4个；
综上所述，图中能数出的直角三角形由6×3+4×3=30（个）；
故选C．
点评：本题考查了等边三角形的性质．解题时，充分利用了三角形中位线定理、等边三角形的“三线合一”的性质．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
（2012•黄陂区模拟）如图，D、E、F分别为等边△ABC中边BC、AC、AB的中点，M是BC边上一动点（不与D点重合）．△EMG是等边三角形，连接CG、DG．下列结论：①S四边形AFME=
